Nous allons encore une fois parler cryptographie dans cet article. Dans l’article précédent, je vous parlais du chiffrement affine, le chiffrement le plus nul après le chiffrement de César, mais cette fois-ci, on va lever le niveau…
Les prérequis
Pour chiffrer un message avec cette méthode, il nous faudra connaître les matrices ainsi que les opérations de base qui s’y rapportent, mais aussi la notion de modulo…
Nous allons nous basé sur un alphabet (un ensemble constitué d’un certain nombre de caractères). Pour ma part, j’ai pris :
alphabet=["A","B","C","D","E","F","G","H","I","J","K","L","M","N","O","P","Q","R","S","T","U","V","W","X","Y","Z",'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z',"'","ù","é","è","à","ç","-","ê"," ","."]
De plus, comme il y a pas mal de calculs d’algèbre linéaires, j’utilise le module numpy.
Condition nécessaire et suffisante
La clé de chiffrement est une matrice. Pour pouvoir chiffrer, et surtout déchiffrer, il faut que le déterminant de cette matrice ait un inverse modulo le nombre de caractères de notre alphabet. Il faut donc, après saisie de la matrice, tester cette condition. Rappelons que le déterminant (que je vais noter d) est inversible modulo n s’il existe un entier x compris entre 0 et n-1 tel que dx = 1 mod n.
De plus, le message à chiffrer doit comporter un nombre de caractères multiple de la dimension de la matrice (qui doit être carrée). Donc ici, deux possibilités :
- soit on demande à l’utilisateur un message ayant un nombre convenable de caractères, ce qui n’est pas très pratique,
- soit on complète le message par des espaces vides afin que le nombre de caractères soit au final un multiple de la dimension de la matrice.
C’est la seconde solution que j’utilise.
Principe du chiffrement
Pour faire simple, je vais prendre une matrice \(2\times2\), par exemple : $$A=\begin{pmatrix}3&7\\2&13\end{pmatrix}$$et un mot de deux lettres, par exemple « MA ».
Première étape
J’attribue à chaque lettre de mon mot un nombre (le rang de la lettre dans l’alphabet). Donc ici, « M » correspond à 12 et « A », à « 0 ». Je créé ainsi un vecteur:$$V=\begin{pmatrix}12\\0\end{pmatrix}.$$
Deuxième étape
Je multiplie la matrice-clé par le vecteur ainsi obtenu:$$\begin{pmatrix}3&7\\2&13\end{pmatrix}\begin{pmatrix}12\\0\end{pmatrix}=\begin{pmatrix}36\\24\end{pmatrix}.$$
Troisième étape
Je prend les coefficients du résultat modulo le nombre de caractères dans l’alphabet. Comme ici c’est 62, ça ne change rien aux nombres obtenus.
Quatrième étape
Je convertis les nombres en caractères en prenant les lettres qui correspondent aux rangs obtenus. Ici, 36 correspond au caractère « k », et 24 à la lettre « Y ».
Le message chiffré est alors : « kY ».
Principe du déchiffrement
Il est le même que celui du chiffrement, en prenant comme matrice l’inverse modulo n de la matrice de chiffrement.
Première étape
On calcule le déterminant de la matrice de chiffrement A. Pour mon exemple, on trouve :$$\det A=25.$$
Ensuite, on exprime la matrice inverse sous la forme :$$A^{-1}=\frac{1}{\det A}B$$où \(B\) doit être trouvée. Pour nous,$$A^{-1}=\frac{1}{25}\begin{pmatrix}13&-7\\-2&3\end{pmatrix}.$$
Deuxième étape
On cherche l’inverse du déterminant modulo le nombre de caractères dans l’alphabet. On cherche donc ici l’inverse de 25 modulo 62. On trouve 5 car \(25\times5=125=1\mod 62\).
Donc on peut écrire:$$A^{-1}=5\begin{pmatrix}13&-7\\-2&3\end{pmatrix}.$$
Troisième étape
On calcule modulo le nombre de caractères dans l’alphabet les coefficients de la matrice inverse. Ici, on obtiens :$$A^{-1}=\begin{pmatrix}65&-35\\-10&15\end{pmatrix}\equiv\begin{pmatrix}3&27\\52&15\end{pmatrix}\mod62.$$
Quatrième étape
On chiffre le message chiffré à l’aide de la matrice inverse. Donc ici, si on part du message « kY », qui correspond au vecteur \(\binom{36}{24}\), on a :$$\begin{pmatrix}3&27\\52&15\end{pmatrix}\begin{pmatrix}36\\24\end{pmatrix}=\begin{pmatrix}756\\2232\end{pmatrix}\equiv\begin{pmatrix}12\\0\end{pmatrix}\mod62.$$On retrouve bien le rang des lettres « M » et « A ».
Résultat en Python
J’ai ici converti en fichier exécutable le programme Python, et voici les captures d’écran:
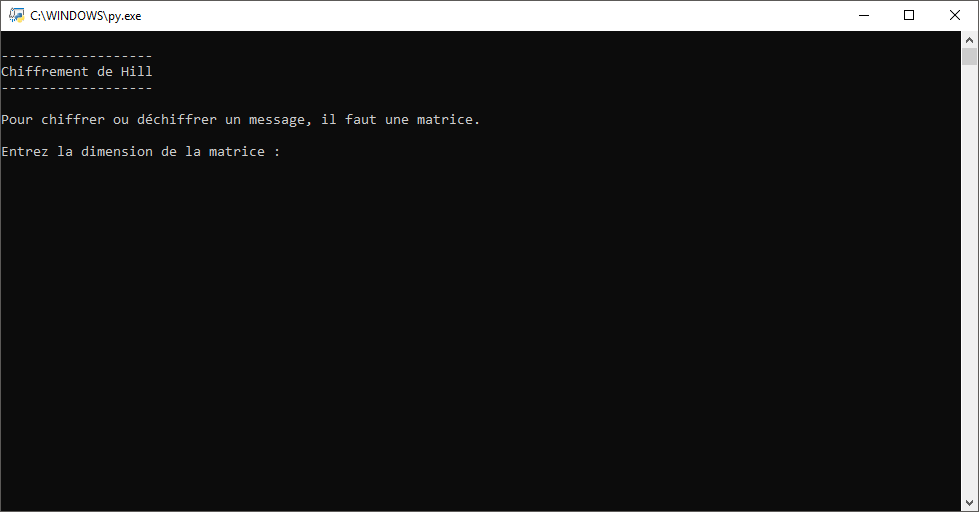
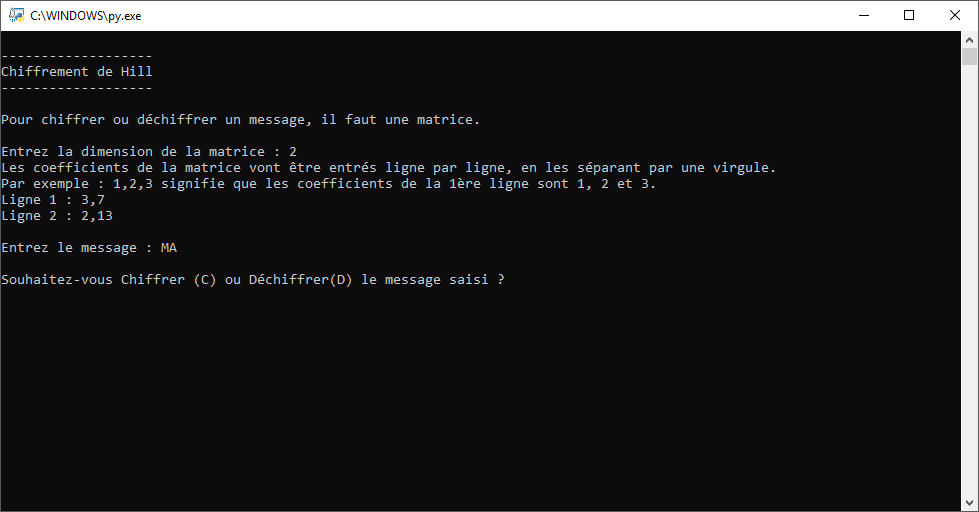
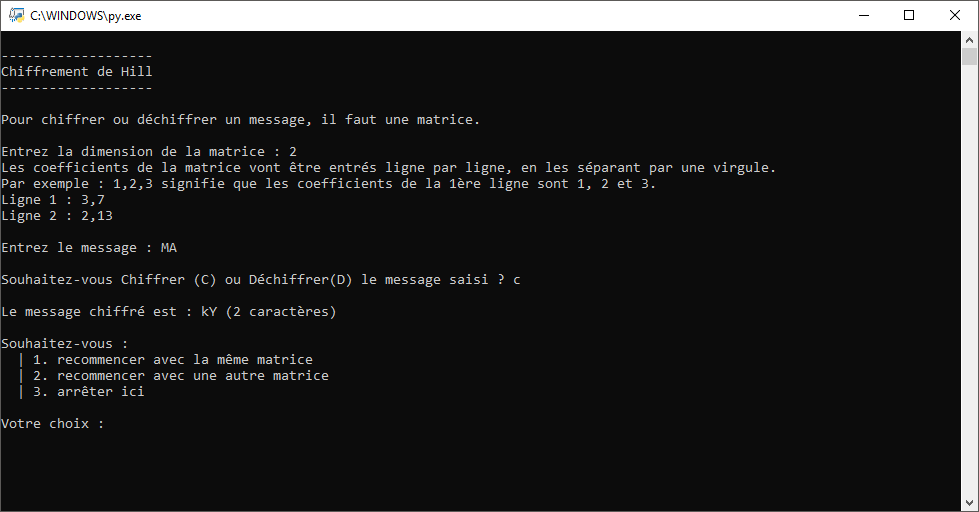
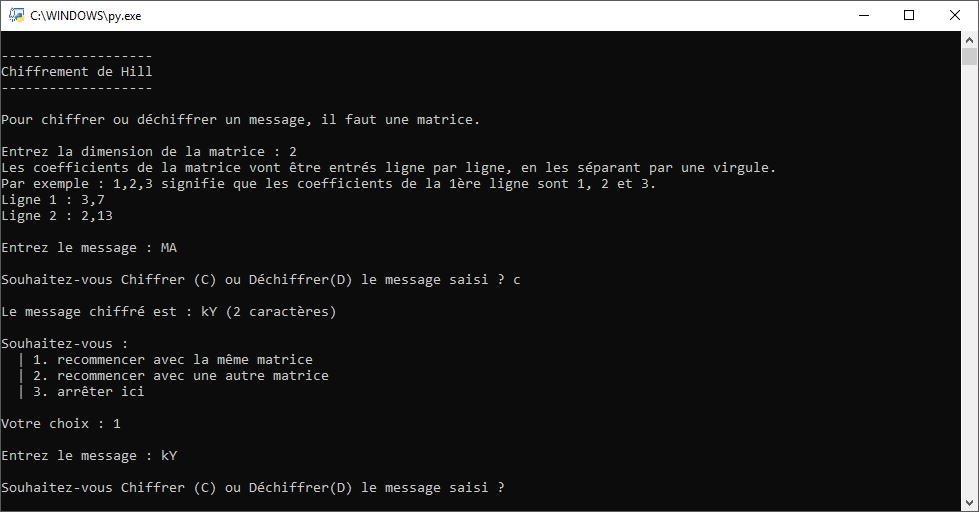
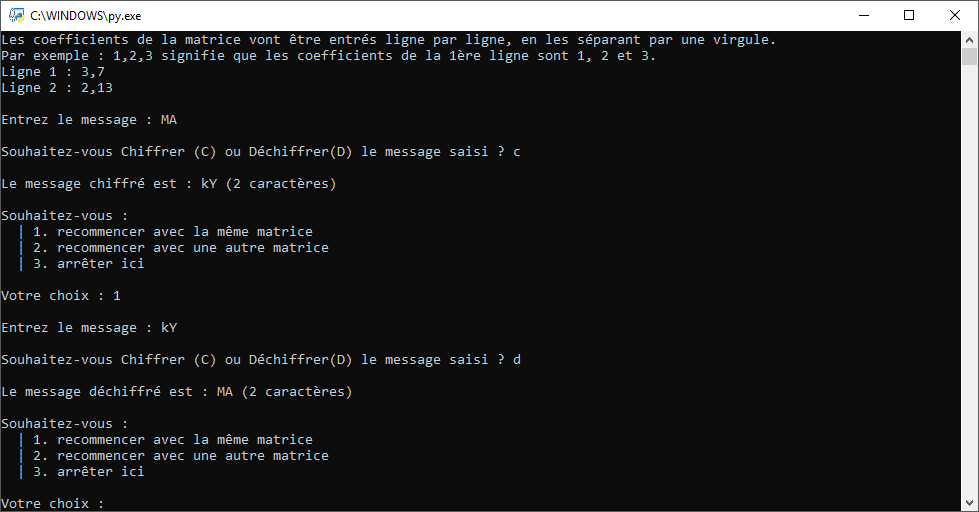
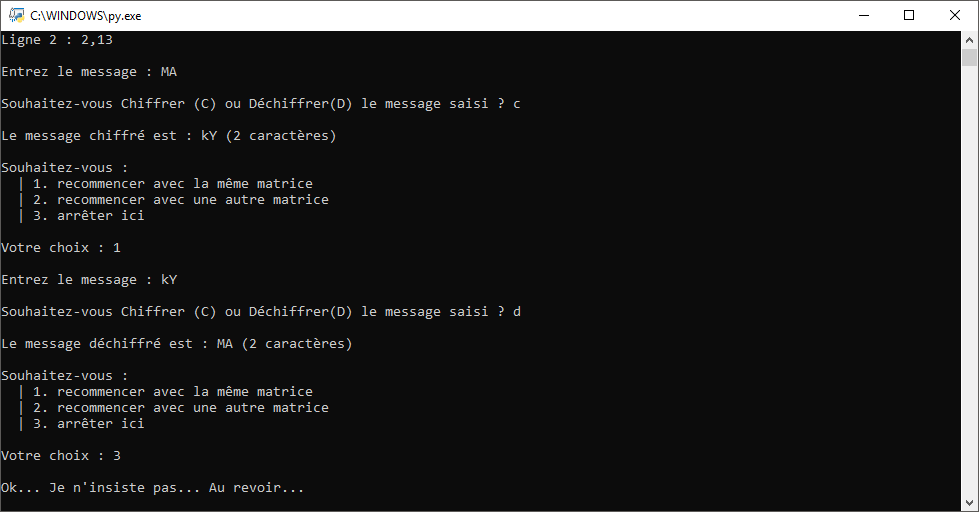
Téléchargement des fichiers
J’ai mis tous les fichiers dans un ZIP ci-dessous. Pour exécuter directement le programme, double-cliquez sur le fichier Hill.py.



Je vais m abonner