Python, turtle et un arbre fractal

Utiliser Python, notamment module turtle, pour construire un arbre fractal, c’est possible ! Je ne suis pas trop fan de ce module (car très lent), mais il faut bien avouer que le résultats est sympatoche… comme disent les jeunes !

Je me suis donc mis à la recherche d’un code donnant un tel schéma pour tenter de me familiariser avec le module. J’avais une idée bien précise : celle d’un arbre fractal, que j’avais vu quelque part.

Après quelques recherches, je suis enfin tombé sur le code suivant (que je me suis permis de commenter):

from turtle import *

angle = 30
color('#3f1905')

def arbre(n,longueur):
    if n==0:
        color('green')
        forward(longueur) # avance
        backward(longueur) # recule
        color('#3f1905')
    else:
        width(n)
        forward(longueur/3) #avance
        left(angle) # tourne vers la gauche de angle degrés
        arbre(n-1,longueur*2/3)
        right(2*angle) # tourne vers la droite de angle degrés
        arbre(n-1,longueur*2/3)
        left(angle) # tourne vers la gauche de angle degrés
        backward(longueur/3) # recule

hideturtle() # cache la tortue
up() # lève le stylo
right(90) # tourne de 90 degrés vers la droite 
forward(300) # avance de 300 pixels
left(180) # fait un demi-tour
down() # pose le stylo
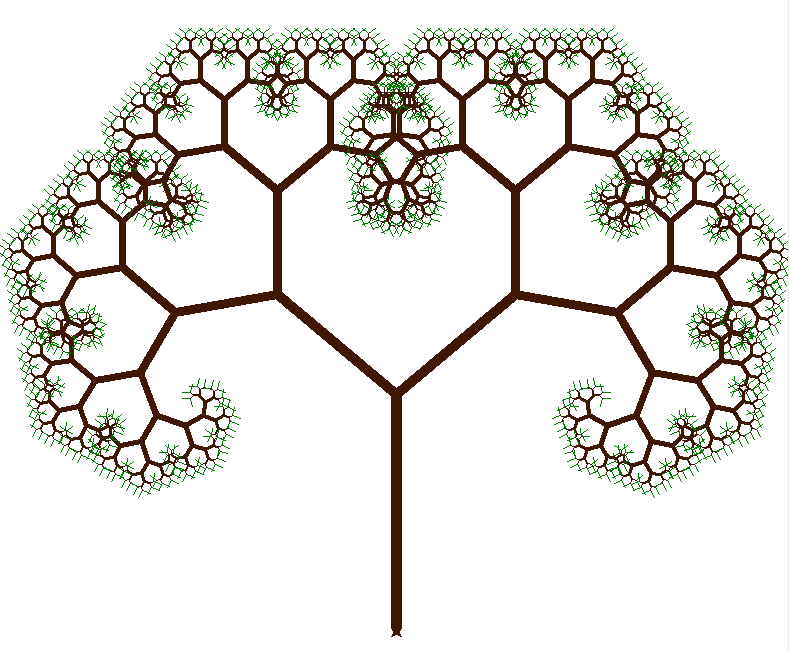
arbre(11,700) # exécute la macro
showturtle() # affiche la tortue
mainloop()

qui donne ceci:

Mais attention… Ce magnifique dessin Python obtenu avec turtle représentant un arbre fractal met un certain temps avant d’être fini (par exemple, sur mon ordinateur 16 Mo de RAM, processeur Intel Core i5, il met une vingtaine de minutes… arf !).

Si on modifie l’angle (disons pour le mettre à 50°), on obtient ceci:

Et avec un angle de 110° :

N’est-il pas choupinou ? 🙂

Vous pouvez remarquer dans le code la fonction récursive : c’est une notion que l’on verra en NSI (nouveau lycée)… mais prévue en cycle de maturité (en Terminale quoi !)… même si je n’ai pas pu résister à l’envie d’en mettre dans mon livre d’exercices corrigés qui sortira en version papier pour la rentrée 2019.

Une fonction récursive est une fonction qui fait appel à elle-même dans sa définition. On retrouve ce genre de fonction par exemple pour calculer le pgcd de deux nombres:

def pgcd(a,b):
    if b==0:
        return a
    else:
        r=a%b
        return pgcd(b,r)
 
print(pgcd(56,42))

Ici, la récursivité s’appuie sur la propriété du pgcd qui stipule que:$$\text{pgcd}(a,b)=\text{pgcd}(b,r)$$où \(a = bq + r,\ 0\leq r < b\).

Les mathématiques sont donc très importantes pour construire des algorithmes (et par suite des programmes) performants. En effet, on aurait très bien pu calculer le pgcd de la manière suivante:

def pgcd(a,b):
    while b<>0:
        r=a%b
        a,b=b,r
    return a
 
print(pgcd(56,42))

Pour comparer deux algorithmes, on parle souvent de complexité. Cet article ne parle pas de cette notion, mais sachez tout de même que la complexité d’une fonction récursive est donnée par une suite arithmético-géométrique. Dans la fonction pgcd, il y a 2 instructions élémentaires (le test sur b et l’affectation de r). La complexité \(C_n\) est donc égale à \(2+C_{n-1}\), où \(C_{n-1}\) est celle de la fonction pgcd(b,r). On démontre alors que la complexité de la fonction récursive est de l’ordre de O(n) [complexité linéaire]. En fait, la complexité est linaire dans le pire des cas (quand a et b sont deux nombres successifs de la suite de Fibonacci), car dans les autres cas, la complexité est logarithmique [O(ln(n))].

L’évaluation moyenne de la complexité de l’algorithme d’Euclide version récursive est assez compliquée. Le nombre d’appels moyen de la fonction pgcd est:$$\frac{12\ln(2\ln n)}{\pi^2}+1,47.$$

http://imss-www.upmf-grenoble.fr/prevert/Prog/Complexite/euclide.html

La complexité de l’algorithme non récursif est quasi-identique à sa version récursive.

La version récursive de l’algorithme d’Euclide est peut-être un peu plus facile à écrire que la version itérative. Les deux versions ont fondamentalement la même complexité, avec un petit avantage à la version itérative, car l’appel d’une fonction n’est pas gratuit.

https://www.labri.fr/perso/betrema/deug/poly/euclide.html

Mais là, je m’égare… Saint-Lazare !