Cet article est principalement destiné aux élèves de 1ère Math Spécialité.

Parlons dans cet article de mathématiques, et plus précisément du second degré. Alors, vous allez me dire : « oui, mais bon ! C’est super simple, il suffit de connaître les formules et on sait tout faire. » Ce n’est pas totalement faux… mais ce n’est pas suffisant ! Il y a beaucoup de situations qui font intervenir le second degré, notamment ce problème…

Une histoire de saut…

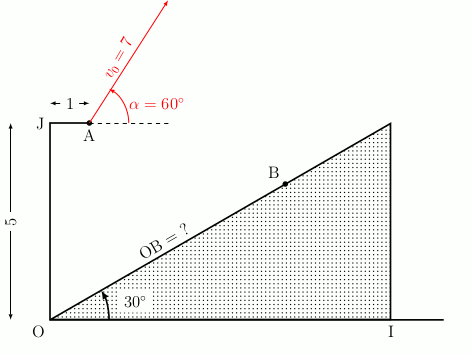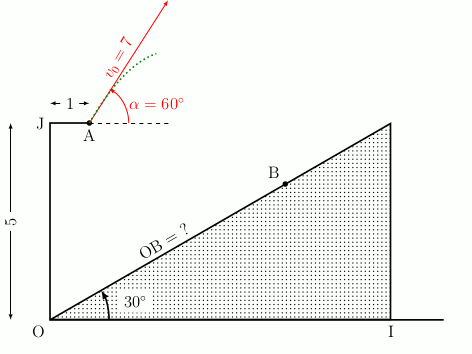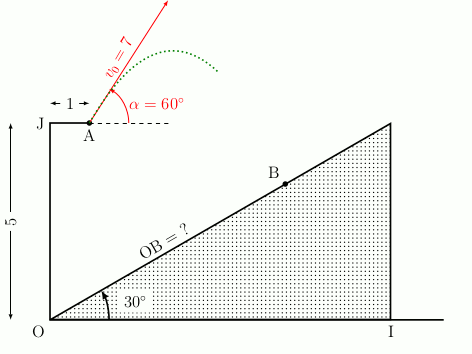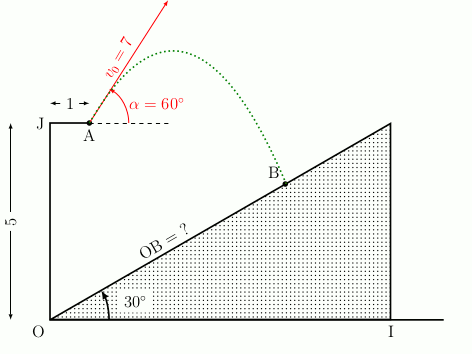
Considérons la situation suivante : une structure est schématisée ci-dessous. Une personne se met au point A et doit sauter afin d’arriver au point B (les longueurs sont exprimées en mètres).

Comment déterminer la distance OB ?

… et de physique

Dès qu’il s’agit de lancer, que ce soit un ballon ou tata Géraldine, c’est Newton qui nous aide à l’aide de ses lois qui (permettez-moi de sauter les détails) nous dit que dans notre situation, la parabole représentant la trajectoire de la personne qui saute admet pour équation (dans le repère d’axes (OI) et (OJ) d’unités 1 mètre) : $$y = -\frac{g}{2v_0^2\cos^2(\alpha)}(x-1)^2+\tan(\alpha)(x-1) + y_0$$ où:

• \(g\) est l’accélération de la pesanteur. Sur Terre, on considère que \( g\approx 10\text{ m}\cdot\text{s}^{-2}\);
• \(v_0\) est la vitesse initiale à laquelle se lance la personne;
• \(\alpha\) est l’angle que forme la tangente à la parabole avec l’horizontale;
• \(y_0\) est la hauteur à partir de laquelle la personne se lance.

On obtient alors, dans notre situation, après avoir remplacé les variables par leur valeur:$$y=\frac{1}{49}\left[-20x^2 + \big( 40+49\sqrt3 \big)x + 225-49\sqrt3 \right].$$

Pour résoudre notre problème, il faut trouver les coordonnées de B, donc de l’intersection de la parabole avec la droite (OB). Cette dernière a pour équation:$$y=\frac{1}{\sqrt3}x.$$ En effet, c’est une droite qui passe par l’origine du repère (donc elle représente une fonction linéaire d’équation \(y=ax\)) et le coefficient directeur est l’accroissement des ordonnées quand on avance d’une unité en abscisse. L’angle du « tremplin » étant de 30 degrés, le coefficient directeur est égal à \(a=\tan(30^\circ)\). Si on ne connaît pas la valeur de \(\tan(30^\circ)\), on peut se ramener aux sinus et cosinus :$$a=\frac {\sin30^\circ}{\cos30^\circ}=\frac{\sqrt3/2}{1/2}=\frac{1}{\sqrt3}.$$ On obtient finalement que l’équation de (OB) est:$$ \frac{1}{\sqrt3} x.$$

Trouver l’abscisse de B revient à résoudre alors l’équation:$$ \frac{1}{\sqrt3}x = \frac{1}{49}\left[-20x^2 + \big( 40+49\sqrt3 \big)x + 225-49\sqrt3 \right].$$Et après avoir multiplié par 49 chaque membre de cette dernière équation, puis tout mis du même côté par rapport au signe « = », on obtient l’équation:$$-20\sqrt3x^2+\big(40\sqrt3+98\big)x+225\sqrt3-147=0.$$

Là, on est en terrain connu (et non en terre inconnue, enfin… je l’espère pour vous !). On sort l’artillerie lourde : discriminant et calcul de racines. Le discriminant est:$$\begin{align}\Delta&=b^2-4ac\\&=(40\sqrt3+98)^2-4\times(-20\sqrt3)\times(225\sqrt3-147)\\&=68404-3920\sqrt3>0\end{align}$$ donc les deux solutions de l’équations sont:$$x_1=\frac{-b-\sqrt\Delta}{2a}=\frac{-(40\sqrt3+98)-\sqrt{ 68404-3920\sqrt3 }}{-40\sqrt3}\approx5,997$$et$$ x_2=\frac{-b+\sqrt\Delta}{2a}=\frac{-(40\sqrt3+98)+\sqrt{ 68404-3920\sqrt3 }}{-40\sqrt3}\approx -1,168.$$ \(x_2<0\) donc cette valeur ne peut pas convenir à notre problème. Ainsi,$$x_B\approx5,997.$$ Il en résulte alors que:$$y_B=\frac{1}{\sqrt3}x_B\approx3,462.$$

Il ne reste plus qu’à calculer maintenant la longueur OB:$$OB\approx\sqrt{5,997^2+3,462^2}\approx6,92.$$

Avec Python

def f(x):
    return (-20*x**2+(40+49*3**0.5)*x+225-49*3**0.5)/49

def g(x):
    return x/(3**0.5)

x = 1

while abs(f(x)-g(x)) > 0.001:
    print(x,f(x),g(x))
    x += 0.0001

print(x)

Ce programme commence par définir deux fonctions f et g (qui correspondent respectivement à la fonction du second degré représentant la trajectoire de la personne qui saute et au tremplin). Pour ne pas faire appel au module math de Python, je me suis permis ici de calculer la racine carrée de 3 en écrivant « 3**0.5 » (qui est équivalent à sqrt(3), soit à \(\sqrt3\)).

Ensuite, on fixe la valeur de x à 1 (car la personne saute à partir d’un point dont l’abscisse est 1, donc inutile de commencer à 0). Je fais ensuite une boucle conditionnelle (while) : tant que la différence entre f(x) et g(x) est strictement supérieure à 0,001, j’ajoute à x 0,0001. Notons que quand on écrit « abs(f(x)-g(x)) », cela signifie que l’on considère la différence sans tenir compte du signe (valeur absolue de la différence : sans signe « moins »).

Si on fait tourner ce programme, on a le temps de se faire chauffer un petit chocolat chaud avec un petit marshmallow, de le boire tranquillement, de faire un peu de gymnastique (le sport, c’est important !) pour enfin voir le résultat : x = 5.996999999999774 (en enlevant le « print » de la boucle, ça doit aller un peu plus vite, mais rester devant un écran où rien ne se passe pendant plusieurs secondes, je trouve ça angoissant…). Remarquez qu’en arrondissant au millième, on obtient bien \(x \approx 5,997\).

Avec Xcas

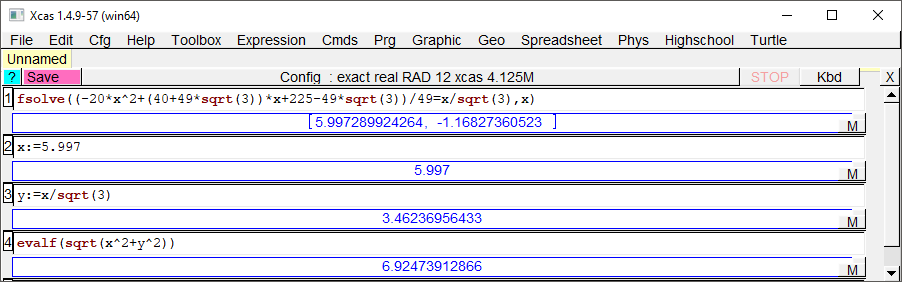
Xcas est un logiciel de calcul formel qui permet bien des choses en mathématiques. Il est téléchargeable gratuitement, donc abusez-en ! Et pour résoudre notre problème (l’équation f(x) = g(x)), on a:

La fonction « fsolve(f(x) = g(x) , x) » nous permet d’obtenir les valeurs approchées des solutions. Je prends donc la valeur qui correspond à ce que nous cherchions (x:=5.997). Ensuite, je définis y comme étant le quotient de x par \(\sqrt3\) et je calcule la longueur OB.