Cet article est inspiré d’un problème tiré du 7ème Championnat International des Jeux Mathématiques et Logiques ( demi-finale, 20 mars 1993).
Le tour
On dispose de six cartes A, B, C, D, E et F sur lesquelles sont mis des nombres de -19 à +19. Une personne choisi un nombre au hasard compris entre -19 et +19 et dit sur quelles cartes ce nombre se trouve. Grâce à cela, on est capable de dire le nombre choisi.
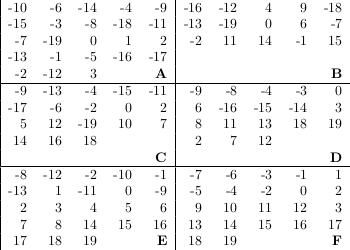
Explications
À chaque carte, nous avons au préalable associé un nombre : \(x_1\) pour la carte A, \(x_2\) pour la carte B, etc.
En ajoutant uniquement les \(x_i\) des cartes où figurent le nombre choisi au hasard, on obtient justement ce nombre. Il ne reste plus qu’à trouver les \(x_i\)…
Pour cela, il suffit de prendre 6 nombres au hasard: je vais prendre 0, 1, -1, 2, -2 et 3.
- « 0 » apparaît sur toutes les cartes, donc:$$x_1+x_2+x_3+x_4+x_5+x_6=0.$$
- « 1 » apparaît sur les cartes A, E et F donc:$$x_1+x_5+x_6=1.$$
- « -1 » apparaît sur les cartes A, B, E et F donc:$$x_1+x_2+x_5+x_6=-1.$$
- « 2 » apparaît sur les cartes A, C, D, E et F donc:$$x_1+x_3+x_4+x_5+x_6=2.$$
- « -2 » apparaît sur les cartes A, B, C, E et F donc:$$x_1+x_2+x_3+x_5+x_6=-2.$$
- « 3 » apparaît sur les cartes A, D, E et F donc:$$x_1+x_4+x_5+x_6=3.$$
Nous avons 6 équations à 6 inconnues, mais si on cherche à résoudre le système formé par ces 6 équations, on n’arrivera pas à trouver toutes les inconnues. On peut seulement obtenir:$$x_2=-2,\ x_3=-1,\ x_4=2.$$ En effet, on arrive à montrer que \(x_1=1-x_5-x_6\) sans obtenir \(x_5\) et \(x_6\). Il nous faut donc prendre d’autres nombres.
- « 19 » apparaît sur les cartes D, E et F donc:$$x_4+x_5+x_6=19\text{ soit }x_5+x_6=17.$$
- « 4 » apparaît sur les cartes B et E donc:$$x_2+x_5=4\text{ soit }x_5=6.$$
On en déduit alors que:$$x_6=11$$et donc que:$$x_1=1-6-11=-16.$$


