Le problème est le suivant: étant donné un carré ABCD de côté 10, on choisit deux points E et F respectivement sur [AD] et [BC] tels que ED = BF = x. On note G le point d’intersection de [BE] et [AF]. L’angle \(\widehat{AGB}\) est-il constant ? Si oui, que vaut sa mesure ? Si non, entre quelles valeurs varie sa mesure ?
Rapportons le carré au repère orthonormé \(A;\vec{AB},\vec{AD}\). Dans ce repère, on a :$$\begin{align}\vec{FA}\cdot\vec{EB}&=\binom{-10}{-x}\cdot\binom{10}{x-10}\\&=-100-x(x-10)\\&=-x^2+10x-100. \quad(1)\end{align}$$
Maintenant, utilisons la formule:$$\vec{u}\cdot\vec{v}=\|\vec{u}\|\times\|\vec{v}\|\times\cos\left(\vec{u},\vec{v}\right)$$pour calculer le même produit scalaire: $$\begin{align}\vec{FA}\cdot\vec{EB}&=FA \times EB \times \cos\alpha\\&=\sqrt{x^2+100}\times\sqrt{100+(10-x)^2}\times\cos\alpha\\&=\sqrt{(x^2+100)(x^2-20x+200)} \times \cos\alpha.\quad (2) \end{align}$$
Des résultats (1) et (2), on peut établir l’égalité:$$ -x^2+10x-100 = \sqrt{(x^2+100)(x^2-20x+200)} \times \cos\alpha$$et en déduire que:$$\cos\alpha=\frac{-x^2+10x-100}{ \sqrt{(x^2+100)(x^2-20x+200)}}.$$
On peut ainsi répondre à la première question: l’angle \(\alpha\) n’est pas constant car son cosinus ne l’est pas.
Répondre à la seconde est bien plus compliquée si on veut le faire algébriquement. En effet, en dérivant la fonction en x obtenue pour le cosinus de \(\alpha\), on obtient une fonction qui peut nous freiner (même si au final, on peut trouver son signe, voir remarque en fin d’article). Ci-après, la capture d’écran Xcas donnant cette dérivée:
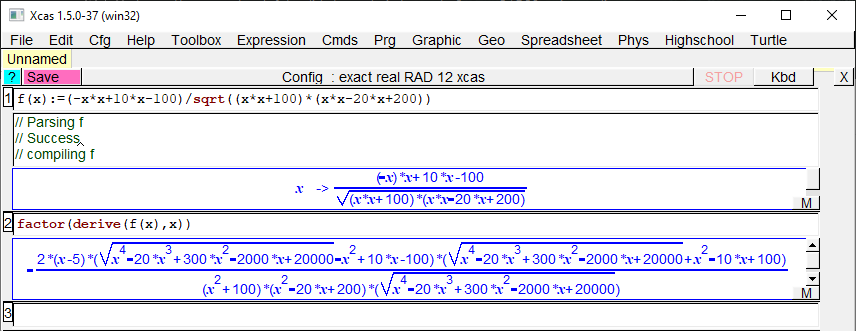
On peut alors avoir envie de tracer la courbe représentative de la fonction à l’aide de GeoGebra:
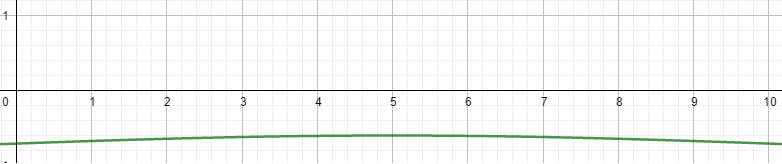
Même en effectuant des supers méga zooms, difficile d’être précis: on peut juste voir que le cosinus ne varie pas beaucoup quand x varie de 0 à 10. On peut alors s’aider d’un programme Python pour définir le minimum et le maximum de la fonction. Mais pour des raisons de symétrie, la courbe est nécessairement symétrique par rapport à x=5. On peut alors dire que f(0) est la valeur minimale et f(5) la valeur maximale. Or,$$f(0)\approx-0,707\quad\text{et}\quad f(5)=-0,6.$$
Ainsi, $$127^\circ < \alpha \leq 135^\circ.$$En effet, \(\arccos(-0,6)=135^\circ\) et \(\arccos(-0,707)\approx 126,86989765\).
Une remarque sur la dérivée
Le passage conjecturant que le minimum et le maximum sont atteints pour x=0 et x=5 n’est pas farfelu; en effet, si on regarde la fonction dérivée donnée par Xcas (sous la forme factorisée), on voit qu’un facteur est égal à (5-x) (il y a un signe « – » avant la fraction donc -(x-5) se transforme en 5-x.
De plus, les autres facteurs du dénominateurs sont positifs sur [0;10]. Il ne reste plus que les deux facteurs du numérateurs de la forme:$$\sqrt{u(x)}-v(x)$$et$$\sqrt{u(x)}+v(x)$$en posant$$u(x)=x^4-20x^3+300x^2-2000x+20000\text{ et }v(x)=x^2-10x+100$$qui, en développant leur produit, donne:$$x^4-20x^3+300x^2-2000x+20000-(x^2-10x+100)^2$$c’est-à-dire:$$400x^2-4000x+10000\geq0.$$On peut donc montrer que f‘(x) est positive sur [0;5] et donc que f est croissante sur cet intervalle.


