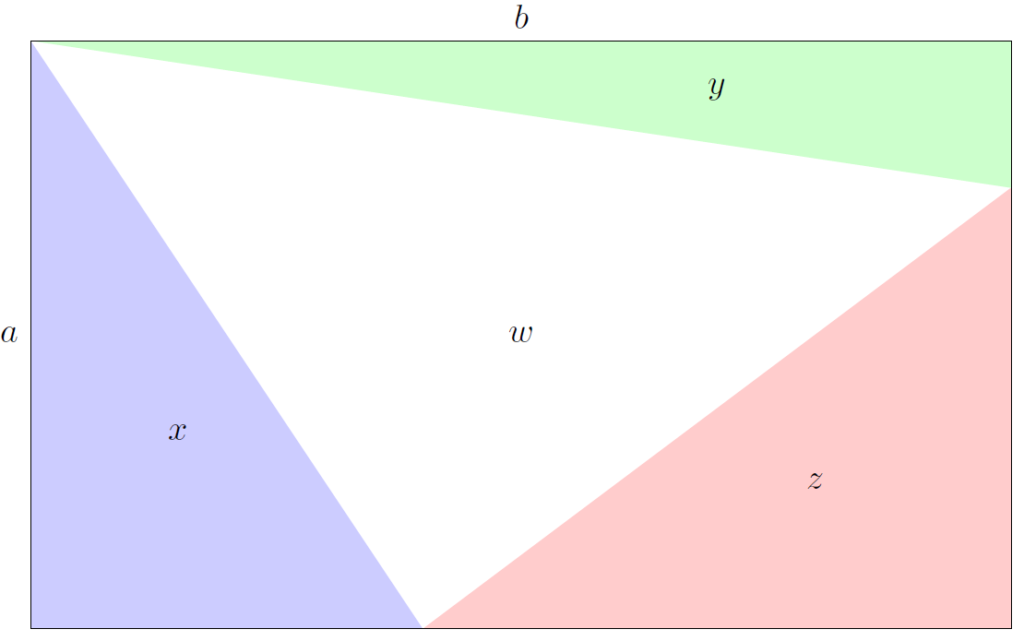
Comment exprimer en fonction de x, y et z l’aire w ?
Ce problème peut être abordé comme application dans le chapitre des polynômes de degré 2…
Étape 1
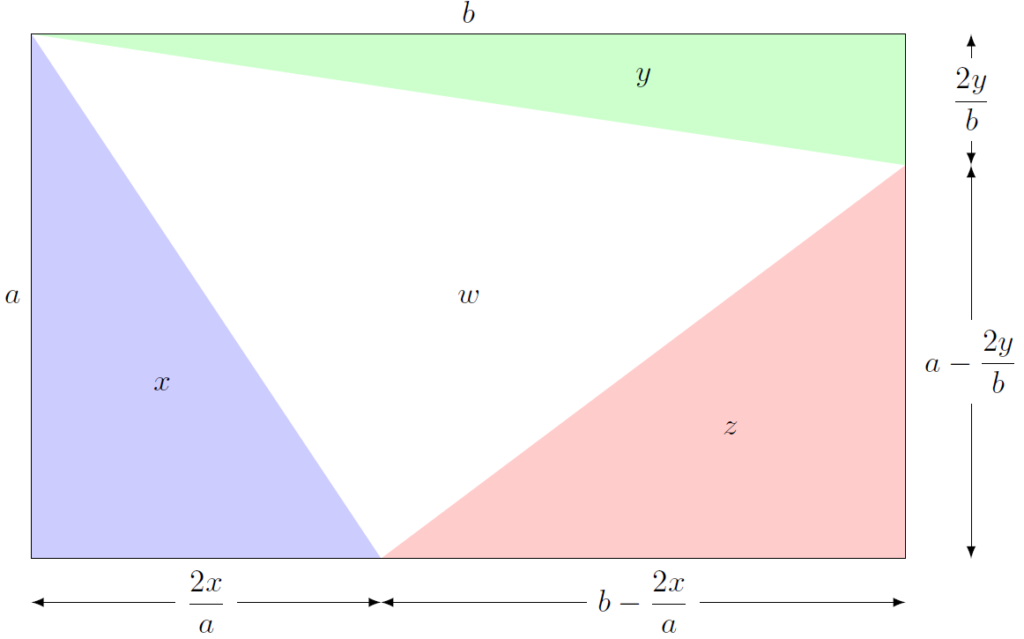
Regardons d’abord le triangle bleu d’aire x : c’est un triangle rectangle de côtés perpendiculaires de mesure a et t, tels que:$$\frac{1}{2}at=x,$$donc:$$t=\frac{2x}{a}.$$
Étape 2
Regardons à présent le triangle vert, d’aire y : il est aussi rectangle et le côté de droite vaut (on utilise le même raisonnement qu’à l’étape 1) :$$\frac{2y}{b}.$$
Étape 3
On déduit maintenant les dimensions restantes:
Ainsi, l’aire du triangle rouge valant z, on a l’égalité:$$\frac{1}{2}\left(b-\frac{2x}{a}\right)\left(a-\frac{2y}{b}\right)=z$$que l’on peut aussi écrire, en multipliant par 2 les deux membres de l’égalité:$$\left(b-\frac{2x}{a}\right)\left(a-\frac{2y}{b}\right)=2z.$$En développant le membre de gauche, on arrive à:$$ab-2y-2x+\frac{4xy}{ab}=2z$$ou encore:$$ab-2(x+y+z)+\frac{4xy}{ab}=0.$$En multipliant maintenant par ab les deux membres de cette dernière égalité, on obtient:$$(ab)^2-2(x+y+z)(ab)+4xy=0.$$
Étape 4
Posons T = ab dans cette dernière égalité. Alors, on a:$$T^2-2(x+y+z)T+4xy=0.$$C’est une équation quadratique d’inconnue T dont les solutions peuvent être:$$T_{1,2}=\frac{2(x+y+z)\pm\sqrt{4(x+y+z)^2-16xy}}{2}$$ soit:$$T_{1,2}=(x+y+z)\pm\sqrt{(x+y+z)^2-4xy}.$$ Ne perdons pas de vue que T = ab = x+y+z+w et donc que:$$T>x+y+z.$$Ainsi, la seule solution possible est:$$T=(x+y+z)+\sqrt{(x+y+z)^2-4xy}.$$On en déduit alors que:$$\boxed{w=\sqrt{(x+y+z)^2-4xy}}$$
Code \(\LaTeX\) de la figure
\documentclass{standalone}
\usepackage{pas-math}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\clip (-0.5,-1) rectangle (11.5,6.5);
\draw (0,0) rectangle +(10,6);
\node[left] at (0,3) {$a$};
\node[above] at (5,6) {$b$};
\fill[blue!20] (0,0) -- (0,6) -- (4,0) -- cycle;
\fill[red!20] (4,0) -- (10,0) -- (10,4.5) -- cycle;
\fill[green!20] (0,6) -- (10,6) -- (10,4.5) -- cycle;
\draw (0,0) rectangle +(10,6);
\node at (1.5,2) {$x$};
\node at (8,1.5) {$z$};
\node at (7,5.5) {$y$};
\node at (5,3) {$w$};
\draw[<->,>=latex] (0,-0.5) -- (4,-0.5) node[midway,fill=white] {$\dfrac{2x}{a}$};
\draw[<->,>=latex] (4,-0.5) -- (10,-0.5) node[midway,fill=white] {$b-\dfrac{2x}{a}$};
\draw[<->,>=latex] (10.75,4.5) -- (10.75,6) node[midway,fill=white] {$\dfrac{2y}{b}$};
\draw[<->,>=latex] (10.75,4.5) -- (10.75,0) node[midway,fill=white] {$a-\dfrac{2y}{b}$};
\end{tikzpicture}
\end{document}