En cette fin d’année, les élèves de 1ère abordent éventuellement le produit scalaire. Nous allons en voir une application pour déterminer la valeur d’un angle.

Un peu de mathématiques

Plaçons-nous dans un repère orthonormé, et considérons deux vecteurs \(\vec{u}\) et \(\vec{v}\) comme ci-dessous:

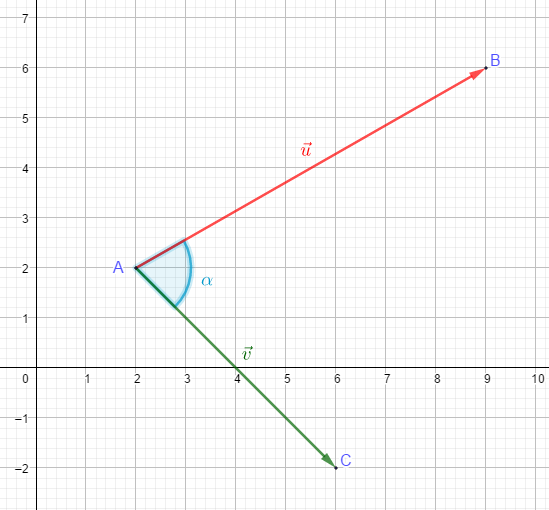
Nous cherchons à déterminer la valeur de l’angle \(\alpha\).

Pour cela, nous allons d’abord calculer le produit scalaire : $$\vec{u}\cdot\vec{v} = xx’ + yy’ = 7\times4 + 4\times(-4) = 12.$$

En effet, \(\vec{u}\displaystyle\binom{7}{4}\) car il faut avancer de 7 unités en abscisse et de 4 unités en ordonnées pour aller du point A au point B. De même, \(\vec{v}\displaystyle\binom{4}{-4}\).

Or, nous savons aussi que:$$\vec{u}\cdot\vec{v}=\|\vec{u}\| \times \|\vec{v}\| \times \cos(\vec{u},\vec{v}).$$ Or, $$\|\vec{u}\| = \sqrt{x_{\vec{u}}^2+y_{\vec{u}}^2}=\sqrt{7^2 + 4^2} = \sqrt{65}$$ et $$\|\vec{v}\| = \sqrt{x_{\vec{v}}^2+y_{\vec{v}}^2}=\sqrt{4^2 + (-4)^2} =4\sqrt{2}.$$Donc:$$\underbrace{\vec{u}\cdot\vec{v}}_{=12}=\sqrt{65}\times4\sqrt{2}\times\cos(\vec{u},\vec{v})$$soit:$$12=4\sqrt{130}\cos(\vec{u},\vec{v}).$$On en déduit alors:$$\cos(\vec{u},\vec{v})=\frac{12}{4\sqrt{130}}$$et donc :$$\alpha=\arccos\left( \frac{12}{4\sqrt{130}}\right)\approx75^\circ.$$

En Python

Nous venons de voir à l’instant une méthode que l’on peut généraliser pour écrire une fonction Python retournant une valeur approchée de l’angle en degrés.

from numpy import arccos,sqrt,pi

def calcAngle(u,v): # u = (a,b) et v = (c,d)
    prodscal = u[0] * v[0] + u[1] * v[1]
    NormeU = sqrt(u[0]**2 + u[1]**2)
    NormeV = sqrt(v[0]**2 + v[1]**2)
    return arccos( prodscal / (NormeU * NormeV) ) * 180 / pi

u = (7,4)
v = (4,-4)
print(calcAngle(u,v))