La suite de Héron est une suite permettant de trouver une valeur approchée d’une racine carrée.

Elle tire son nom du mathématicien Héron d’Alexandrie.

Suite de Héron: étude mathématique

On considère la suite \((u_n)_{n\in\mathbb{N}}\) définie par son premier terme \(u_0 > 0\) et par la relation de récurrence suivante :$$\forall n\in\mathbb{N},\quad u_{n+1}=\frac{1}{2}\left(u_n+\frac{a}{u_n}\right)$$où \(a\) est un réel strictement plus grand que 0 (le cas où il est égal à 0 ne nous importe peu car la suite devient géométrique de raison \(\frac{1}{2}\) et converge donc vers 0).

Cette suite est appelée une suite de Héron de paramètre a.

Fonction associée à la suite de Héron

Immédiatement, on peut constater que \(u_{n+1} = f(u_n)\), avec:$$f(x)=\frac{1}{2}\left(x+\frac{a}{x}\right)$$que l’on peut définir sur \(]0;+\infty[\).

Sa dérivée est alors:$$f'(x)=\frac{1}{2}\left(1-\frac{a}{x^2}\right)$$que l’on peut aussi écrire:$$f'(x)=\frac{x^2-a}{2x^2}.$$

L’expression \(x^2-a\) s’annule pour \(x=-\sqrt{a}\) et pour \(x=\sqrt{a}\). On a alors le tableau de variations suivant :

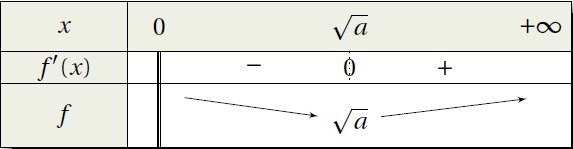
f admet donc un minimum pour \(x=\sqrt{a}\) qui vaut \(\sqrt{a}\).

Pour tout réel x > 0, \(f(x) \geqslant \sqrt{a}\).

Tous les termes de la suite sont positifs

Ce résultat est presque immédiat. En effet, $$u_0>0$$ donc $$\frac{1}{2}\left(u_0 + \frac{a}{u_0}\right)>0$$donc:$$u_1>0.$$

De plus, si on suppose que pour un entier k fixé, \(u_k>0\),$$\frac{1}{2}\left(u_k + \frac{a}{u_k}\right)>0$$donc:$$u_{k+1}>0.$$

D’après le principe de récurrence, on peut conclure que pour tout entier naturel n, \(u_n>0\).

La suite de Héron est minorée par \(\sqrt{a}\)

Nous venons en effet de démontrer que tous les termes de la suite sont strictement positifs donc pour tout entier naturel n, \(f(u_n) \geqslant \sqrt{a}\) d’après les variations de la fonction f.

La suite est décroissante

En effet, on a:$$\begin{align}u_{n+1}-u_n & = \frac{1}{2}\left(u_n+\frac{a}{u_n}\right)-u_n\\&=\frac{1}{2}\left(u_n+\frac{a}{u_n}\right)-\frac{1}{2}\times2u_n\\&=\frac{1}{2}\left(u_n+\frac{a}{u_n}-2u_n\right) \\&=\frac{1}{2}\left(\frac{a-u_n^2}{u_n}\right)\end{align}$$

Or, nous avons vu précédemment que pour tout entier naturel n > 0, \(u_n\geqslant\sqrt{a}\), donc que \(u_n^2 \geqslant a\), ce qui nous assure que \(u_{n+1}-u_n \leqslant 0\) pour n > 0.

Cette suite est donc décroissante à partir de n = 1.

La suite est convergente

La suite est minorée et décroissante. D’après le théorème de convergence des suites monotones, elle converge donc. Notons \(\ell\) sa limite.

Comme f est une fonction continue, on peut écrire : $$u_{n+1} = f(u_n) \Rightarrow \lim\limits_{n\to+\infty} u_{n+1} = f\left(\lim\limits_{n\to+\infty} u_n\right),$$c’est-à-dire:$$\ell = f(\ell).$$On doit donc résoudre cette dernière équation pour déterminer la valeur de la limite de la suite.

$$\begin{align}\ell = f(\ell) & \iff \ell = \frac{1}{2}\left(\ell + \frac{a}{\ell}\right)\\&\iff 2\ell = \ell + \frac{a}{\ell}\\&\iff \ell = \frac{a}{\ell}\\&\iff \ell^2=a\\&\iff \ell=-\sqrt{a}\text{ ou }\ell = \sqrt{a} \end{align}$$

Or, tous les \(u_n\) sont positifs donc \(\ell\) ne peut pas être égale à \(\sqrt{a}\). Par conséquent,$$\lim\limits_{n\to+\infty} u_n=\sqrt{a}.$$

Vitesse de convergence de la suite de Héron

Effectuons le calcul suivant:$$\begin{align}u_{n+1}-\sqrt{a} & = \frac{1}{2}\left( u_n + \frac{a}{u_n} \right) – \sqrt{a} \\ & = \frac{1}{2}\left( u_n + \frac{a}{u_n} \right) – \frac{1}{2}\times2\sqrt{a}\\&=\frac{1}{2}\left( u_n + \frac{a}{u_n} – 2\sqrt{a}\right)\\&=\frac{1}{2}\left( \frac{u_n^2 + a – 2\sqrt{a} }{u_n} \right) \\& = \frac{1}{2}\times\frac{\left(u_n-\sqrt{a}\right)^2}{u_n} \end{align}$$

Or, on sait que \(u_n \geqslant \sqrt{a} \) pour n > 0, donc \(\frac{1}{u_n} \leqslant \frac{1}{\sqrt{a}}\), ce qui donne alors:$$u_{n+1}-\sqrt{a} \leqslant \frac{\left(u_n-\sqrt{a}\right)^2}{2\sqrt{a}}$$

ce qui signifie que d’un terme à l’autre, le nombre de décimales correctes double. On dit que la convergence est quadratique.

Suite de Héron: du côté de Python

Voici un exemple de programme Python:

def heron(a,p):
    u = 3 # premier terme quelconque strictement positif
    delta = 1
    n = 0
    while delta >= 10**(-p):
        prec = u
        u = 0.5 * (u + a/u)
        delta = abs(prec - u)
        n += 1
        
    return u,n

J’ai ici implémenté une fonction heron(a,p) qui admet deux arguments : « a » est le nombre dont on cherche une valeur approchée à \(10^{-p}\) de sa racine carrée.

Il est à noter toutefois qu’il est inutile de mettre de trop grandes valeurs de p car Python est assez limité dans les décimales.

Ce programme donne par exemple:

>>> heron(11,7)
(3.3166247903554, 5)
>>> heron(999,10)
(31.606961258558215, 8)
>>> heron(0.5,8)
(0.7071067811865475, 8)

Cela signifie que 5 termes ont suffit pour trouver la valeur approchée de \(\sqrt{11}\) à 7 chiffres significatifs, et que 8 ont suffit pour trouver la valeur approchée de \(\sqrt{999}\) et \(\sqrt{0,5}\) à 8 chiffres significatifs.