Dans la catégorie « notions qui n’est plus enseignée en mathématiques au lycée » (tiens… ça aurait été une bonne idée de créer cette catégorie sur ce site!), celle de barycentre est à mes yeux d’une rare beauté.
Nous allons voir dans cet article les grandes lignes ainsi que les raisons pour lesquelles cette notion est importante dans certaines sciences.
La notion de barycentre: introduction mathématique
Système pondéré
En mathématiques, on appelle système pondéré tout ensemble d’éléments affecté d’un nombre, que l’on appelle poids.
L’exemple le plus simple est un système composé de notes de devoirs, chaque note étant affecté d’un coefficient en fonction de l’importance du devoir.
Si Choupinette a obtenu 15/20 (coef. 3), 13/20 (coef. 2) et 18/20 (coef. 1) en mathématiques au cours d’un trimestre, on peut considérer que ces trois notes constitue le système pondéré:$$\{(15,3)~;~ (13,2)~;~(18,1)\}.$$
Barycentre d’un système pondéré
Le barycentre d’un système pondéré peut être considéré comme une moyenne du système (en fait, une moyenne arithmétique est un barycentre).
Si on considère le système pondéré \(\{(x_k,\alpha_k)\}_{1\leqslant k\leqslant n}\), son barycentre est:$$\text{bar}\{(x_k,\alpha_k)\}_{1\leqslant k\leqslant n}=\frac{1}{\displaystyle\sum_{k=1}^n\alpha_k}\sum_{k=1}^n \alpha_kx_k.$$
Pardon ? Que me dis-tu là ? Et oui… ça ressemble fortement à une formule de statistique non ? Ben oui ! C’est la formule qui donne la moyenne pondérée (je vous avais prévenu !).
En fait, la notion de barycentre est plus lié à la géométrie qu’aux calculs, mais l’idée est la même: étant donné un système pondéré de points \( \{ (A_k,\alpha_k) \}_{1\leqslant k\leqslant n} \), on définit le barycentre des n points comme étant le point G tel que:$$\sum_{k=1}^n \alpha_k\overrightarrow{GA_k}=\overrightarrow{0}.$$
Le barycentre en astronomie
Notre système solaire, tout comme n’importe quel système physique, a un barycentre. Tous les corps célestes ont une masse et donc constituent un système pondéré, qui admet un barycentre.
Si l’on ne considère que le système composée des planètes et de notre étoile (le Soleil) (les autres corps étant de masse négligeable par rapport à celle des éléments de ce système), tous ces gravitent, tournent, autour d’un point: le barycentre (représenté en vert dans la vidéo ci-dessus).
Ce constat est intéressant à deux points de vue:
- d’abord, le Soleil n’est pas le barycentre de notre système, donc la prochaine fois que vous voulez briller en société, ne dites pas que toutes les planètes tournent autour du Soleil mais qu’elle tournent autour d’un point qui est très proche du Soleil (en fait, il est quasi à sa surface);
- ensuite, si l’on observe une étoile à l’extérieur de notre système solaire, et que celle-ci semble tourner légèrement autour d’un point, c’est que cette étoile est influencée par d’autres corps célestes de masse conséquente (donc l’observation d’un barycentre d’une étoile situé à l’extérieur de cette étoile montre l’existence éventuelle d’autres planètes).
Le constat est le même si l’on ne considère qu’un système constitué d’une planète et de leurs lunes (comme le système Terre-Lune):
Le barycentre en Physique
La formule mathématique que nous avons vue (avec des symboles de sommation discrète « sigma ») peut être envisagée dans le cas continue (si le nombre de points est infini).
Si le système pondéré devient un ensemble continu D, constitué de points M à densité g(M), g étant une fonction continue (champ scalaire) alors la formule devient:$$\int_D g(M)\overrightarrow{GM}\text{d}S=\overrightarrow{0}$$ pour ce qui est dans le plan, et:$$\int_D g(M)\overrightarrow{GM}\text{d}V=\overrightarrow{0}$$pour ce qui est de l’espace. Concrètement, dans l’espace à 3 dimensions (puisque c’est là que nous vivons), si M a pour coordonnées \((x_1;x_2;x_3)\) alors les coordonnées dy barycentre sont données par les égalités:$$x_{{j,{\mathrm {G}}}}={\frac {\iiint g(x_{1},x_{2},x_{3})\cdot x_{j}~{\mathrm d}x_{1}{\mathrm d}x_{2}{\mathrm d}x_{3}}{\iiint g(x_{1},x_{2},x_{3})~{\mathrm d}x_{1}{\mathrm d}x_{2}{\mathrm d}x_{3}}},\quad j\in \{1,2,3\}.$$
Une propriété mathématique
Soit le système pondéré \(\{(A_k,\alpha_k)\}_{1\leqslant k\leqslant n}\) de barycentre G.
Supposons ce système constitue une partition de deux ensembles disjoints (par exemple, les ensembles \( \{(A_1,\alpha_1);(A_2,\alpha_2);\cdots;(A_{n/2},\alpha_{n/2} )\} \) et \( \{(A_{n/2+1},\alpha_{n/2+1});(A_{n/2+2},\alpha_{n/2+2});\cdots;(A_n,\alpha_n) \} \) pour n pair, de barycentres respectifs \(G_1\) et \(G_2\).
Alors, $$G=\text{bar} \left\{\left(G_1;\displaystyle\sum_{k=1}^{n/2}\alpha_k\right)~;~\left(G_2,\displaystyle\sum_{k=n/2+1}^n\alpha_k \right)\right\}.$$
C’est ce que l’on appelle l’associativité des barycentres et cela nous permet de construire plus simplement le barycentre d’un système constitué de 4 points par exemple:
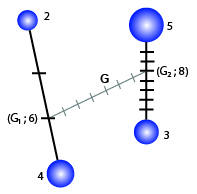
Explications :
- Pour construire \(G_1=\text{bar}\{(A,2)~;~(B,4)\}\), on utilise la relation vectorielle:$$2\overrightarrow{G_1A}+4\overrightarrow{G_1B}=\overrightarrow{0}$$ soit, en utilisant la relation de Chasles:$$2\overrightarrow{G_1A}+4\overrightarrow{G_1A}+4\overrightarrow{AB}=\overrightarrow{0}$$ce qui donne:$$6\overrightarrow{G1A}=4\overrightarrow{BA}$$et donc:$$\overrightarrow{AG_1}=\frac{2}{3}\overrightarrow{AB}.$$
- Pour construire \(G_2=\text{bar}\{(C,3)~;~(D,5)\}\), on procède de même à partir de l’égalité:$$3\overrightarrow{G_2C}+5\overrightarrow{G_2D}=\overrightarrow{0}$$qui donne:$$\overrightarrow{CG_2}=\frac{5}{8}\overrightarrow{CD}.$$
- Pour construire \(G=\text{bar}\{(G_1,6)~;~(G_2,8)\}\), on procède de même à partir de l’égalité:$$6\overrightarrow{GG_1}+8\overrightarrow{GG_2}=\overrightarrow{0}$$qui donne:$$\overrightarrow{G_1G}=\frac{4}{7}\overrightarrow{G_1G_2}.$$
Le système de notation par pouces
Ce système repose sur la notion de barycentre.
Prenons l’exemple d’une plateforme de vidéos bien célèbre (tou doum !). Je ne suis pas dans les confidences de celle-ci mais je vais imaginer qu’à chaque œuvre correspond un dictionnaire d’éléments (genre, réalisateur, acteurs, pays d’origine,…). Imaginons maintenant qu’à chaque fois que l’on met un pouce en l’air pour signifier que l’on a aimé, le compteur de chaque élément soit incrémenté. Au contraire, si on met un pouce vers le bas, les compteurs décrémentent.
Si on souhaite savoir si une autre œuvre a des chances de nous plaire, on peut analyser le système pondéré formé par ses éléments (en fait, là, concrètement, je en vois pas trop comment mais bon… Et vous ? N’hésitez pas à laisser en commentaire vos suggestions).
Document sur la notion de barycentre: https://www.sbpm.be/wp-content/uploads/2017/08/Brochure-barycentres.pdf


