Prenez une ellipse de centre O et mettez sur cette ellipse un point A.
Ensuite, mettez sur cette même ellipse un point M tel que \(\widehat{AOM}=\alpha^\circ\) et un autre point N tel que \(\widehat{AON}=2\alpha^\circ\).
Tracez la perpendiculaire à [MN] passant par O; elle coupe [MN] en B. Tracez alors le cercle de centre M et passant par B.
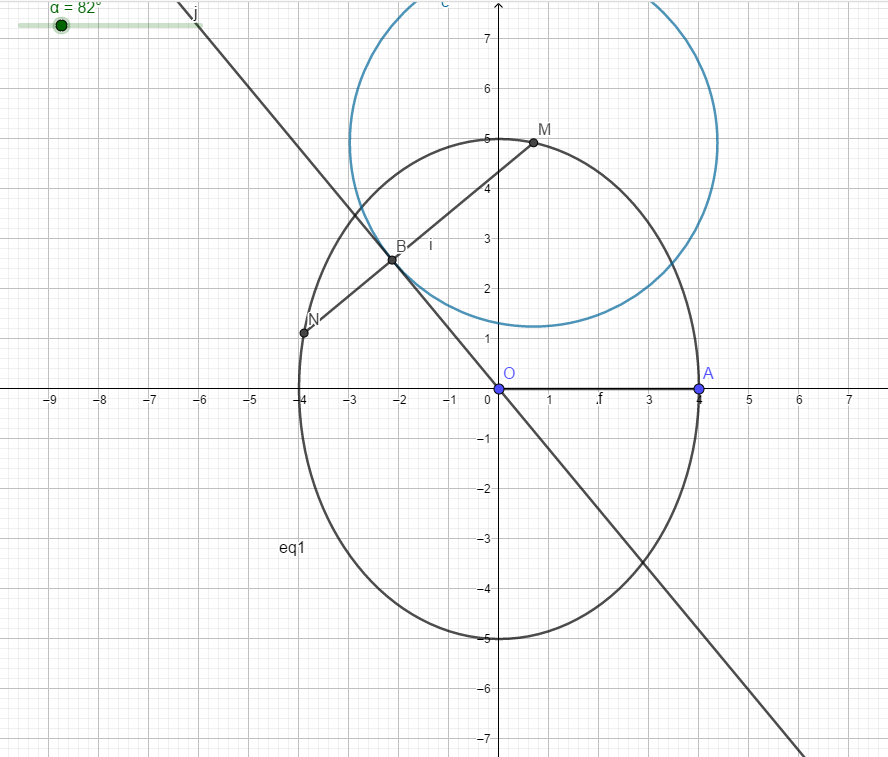
Que se passe-t-il quand on fait varier \(\alpha\) entre 0 et 360 degrés ?
La réponse en vidéo :
Les cercles forment l’enveloppe d’une cloche dans l’ellipse.
Cela ne sert à rien, mais j’ai trouvé plutôt sympa…
Le téléchargement du fichier Geogebra est ci-dessous pour les abonné·e·s:


