J’ai pu constaté ces derniers temps que les outils pour les probabilités en Python au lycée (loi binomiale et variables aléatoires) ne sont pas très pratiques à utiliser.
Probabilités et Python au lycée: loi binomiale et variables aléatoires – Introduction
Je suis en train de rédiger un livre consacré à l’utilisation de Python au lycée en enseignement des mathématiques, et je suis arrivé à la partie “probabilités”. Simuler une loi binomiale n’est pas une chose très naturelle, bien que facile quand on sait comment s’y prendre. De même, je n’ai pas trouvé de modules Python qui offrent la possibilité d’obtenir simplement ce que l’on attend des élèves: \(P(X=k)\), \(P(X \leqslant k)\), … Ce n’est pourtant pas bien compliqué à implémenter… Surtout pour le peu de besoins que nous avons au lycée.
J’ai donc décidé de créer mon module probastat.py que je vais vous exposer ici:
Probabilités et Python au lycée: loi binomiale
La première chose qu’il faut savoir, c’est que j’aime bien la POO. C’est pour cela que j’ai décidé de considérer une variable aléatoire X (qui suit la loi binomiale \(\mathcal{B}(n;p)\)) comme un objet, donc définie par une classe.
Probabilités et Python au lycée (loi binomiale) : le constructeur
class binom:
def __init__(self,n,p):
self.n = n
self.p = p
self.fact = [ 1 ]
for i in range(1,n+1):
self.fact.append( self.fact[i-1] * i )
Remarquez la présence d’une liste un peu spéciale dans le constructeur: cette liste contient toutes les factorielles 0!, 1!, 2!, …, n!
J’ai opté pour cette solution car faire appel à une fonction factorielle rendait les méthodes de la classes plus lentes pour des valeurs de n assez grandes (comme 50).
>>> X = binom(50, 0.3)Ceci déclare une variable X suivant la loi binomiale de paramètres n = 50 et p = 0,3.
Tous les exemples suivants seront basés sur cette variable.
Probabilités et Python au lycée (loi binomiale) : les méthodes
Calcul de l’espérance
def moyenne(self , r = None):
if r != None:
return round(self.n * self.p , r)
else:
return self.n * self.p
Rien de bien compliqué, comme prévu: j’utilise la formule \(E(X)=np\). J’ai seulement mis un argument r au cas où l’on aimerait avoir un résultat arrondi à r chiffres après la virgule.
>>> X.esp()
15.0Calcul de la variance
Là encore, j’utilise la formule du cours : \(V(X)=np(1-p)\).
def var(self , r = None):
if r != None:
return round(self.n * self.p * (1 - self.p) , r)
else:
return self.n * self.p * (1 - self.p)
>>> X.var(2)
10.5Calcul de l’écart-type
Pas de suspens… J’utilise la formule \(\sigma(X)=\sqrt{V(X)}\).
def ecart(self , r = None):
if r != None:
return round(self.var()**0.5 , r)
else:
return self.var()**0.5
>>> X.ecart(2)
3.24Calcul de \(P(X=k)\)
J’utilise la formule de Bernoulli : \( P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}\).
def proba(self,k,r = None):
if r == None:
return ( self.fact[self.n] / ( self.fact[k] * self.fact[self.n - k] ) ) * self.p**k * (1 - self.p)**(self.n-k)
else:
return round( ( self.fact[self.n] / ( self.fact[k] * self.fact[self.n - k] ) ) * self.p**k * (1 - self.p)**(self.n-k) , r)
C’est dans cette méthode que j’utilise la liste des factorielles obtenue dans le constructeur.
>>> X.proba(15)
0.1223468618354011Calcul de \(P(X\leqslant k)\)
def proba_cdf(self,k,r = None):
cdf = 0
for i in range(k+1):
cdf += self.proba(i)
if r == None:
return cdf
else:
return round(cdf , r)
>>> X.proba_cdf(15,3)
0.569Calcul de h telle que \(P(X\leqslant h) = x\)
def proba_icdf(self , pr):
h = 0
while self.proba_cdf(h) < pr :
h += 1
return h
>>> X.proba_icdf(0.95)
20Probabilités et Python: simulation d’une loi binomiale
def simul(self , k , c = None , e = None):
LX = [ i for i in range( self.n + 1) ]
LY = [ 0 ] * (self.n + 1)
for i in range(k):
p = self.proba_icdf( random() )
LY[p] += 1
Y = [i/k for i in LY]
if c != None:
if e != None:
bar(LX,Y,color=c,edgecolor=e)
else:
bar(LX,Y,color=c)
else:
bar(LX,Y)
show()
Pour cette méthode, il faut faire appel à matplotlib.pyplot.
>>> X.simul(1000, 'pink', 'red')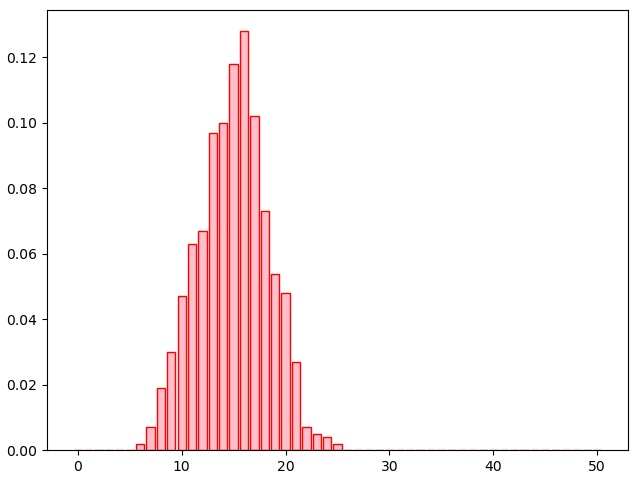
Probabilités et Python: distribution de la loi binomiale
def distrib(self , c = None , e = None):
LX = [ i for i in range( self.n + 1) ]
LY = [ self.proba(k) for k in range( self.n + 1) ]
if c != None:
if e != None:
bar(LX,LY,color=c,edgecolor=e)
else:
bar(LX,LY,color=c)
else:
bar(LX,LY)
show()
Cette méthode permet de construire le diagramme en barres de la distribution de la loi binomiale.
>>> X = binom(50,0.11)
>>> X.distrib('cyan','blue')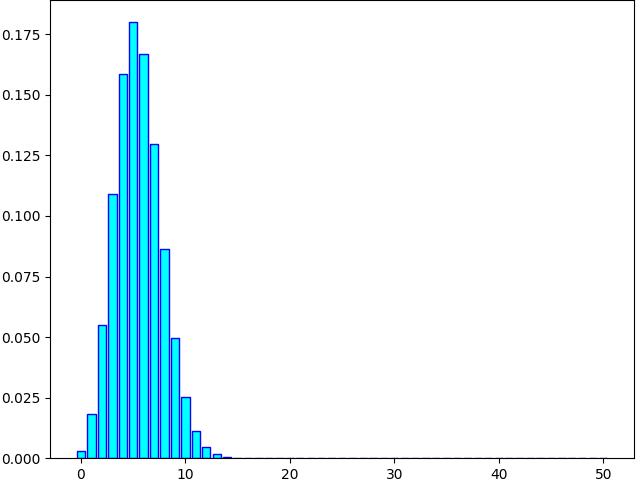
Intervalle de fluctuation
def fluctuations(self , seuil = 0.95):
return interv(self.n, self.p, seuil)
class interv:
def __init__(self,n,p,seuil):
V = binom(n,p)
L = [ V.proba_cdf(k) if V.proba_cdf(k)<1 else 1 for k in range(n+1) ]
self.tableau = '{:>5} | {:^20}\n{:5} | {:>20}'.format('k' , 'P(X ≤ k)' , 0 , V.proba_cdf(0))
a = 0
for k in range(1,n+1):
if L[k-1] < (1-seuil)/2 and L[k] >= (1-seuil)/2:
a = k
elif L[k-1] <= (1+seuil)/2 and L[k] > (1+seuil)/2:
b = k
self.tableau += '\n{:5} | {:>20}'.format( k , L[k] )
self.intervalle = a, b
Cette méthode permet d’avoir le tableau des valeurs de P(X ≤ k), pour 0 ≤ k ≤ n, et d’avoir un intervalle de fluctuation au seuil de 95% (par défaut) ou d’un autre seuil.
J’ai ici opté pour créer un objet “interv” pour que l’appel aux différentes variables soit plus intuitif.
>>> print( X.fluctuations().tableau )
k | P(X ≤ k)
0 | 0.0029478157317550176
1 | 0.02116465452349951
2 | 0.07632687985355727
3 | 0.18541172994445798
4 | 0.3438298970708503
5 | 0.5239638129493998
6 | 0.6909418810390664
7 | 0.820664810341472
8 | 0.9068431046673678
9 | 0.9565489373497197
10 | 0.981736949192125
11 | 0.9930574039527565
12 | 0.9976046652751451
13 | 0.9992474960726891
14 | 0.9997841189736526
15 | 0.9999432970027025
16 | 0.9999863331973543
17 | 0.9999969713578301
18 | 0.9999993818773386
19 | 0.9999998836531322
20 | 0.9999999797798432
21 | 0.9999999967524568
22 | 0.9999999995176578
23 | 0.9999999999337214
24 | 0.9999999999915729
25 | 0.999999999999009
26 | 0.9999999999998928
27 | 0.9999999999999899
28 | 0.9999999999999998
29 | 1
30 | 1
31 | 1
32 | 1
33 | 1
34 | 1
35 | 1
36 | 1
37 | 1
38 | 1
39 | 1
40 | 1
41 | 1
42 | 1
43 | 1
44 | 1
45 | 1
46 | 1
47 | 1
48 | 1
49 | 1
50 | 1
>>> X.fluctuations().intervalle
(2, 10)Les plus averti·e·s d’entre vous auront remarqué la manière dont la liste L a été construite dans la méthode (par compréhension, avec un test). En effet, le test est nécessaire car sans le mettre, on obtient des probabilités supérieures à 1 à la fin du tableau
Probabilités et Python: variables aléatoires
La logique est la même que pour les variables aléatoires qui suivent la loi binomiale. Je vais utiliser la POO.
Le constructeur
class variable:
def __init__(self,X,N):
self.X = X
self.N = N
>>> L = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> P = [0.1, 0.05, 0.2, 0.01, 0.3, 0.04, 0.07, 0.1, 0.03, 0.04, 0.06]
>>> X = variable(L,P)Définie une variable aléatoire prenant ses valeurs parmi les éléments de la liste L, sachant que la probabilité P(X=L[i]) vaut P[i]. Par exemple, ici, P(X = 3) = 0,01.
Les méthodes
Calcul de l’espérance
def esp(self,r = None):
if (len(self.X) != len(self.P)):
return False
e = 0
for i in range( len(self.X) ):
e += self.X[i] * self.P[i]
e /= sum(self.P)
if r != None:
return round(e , r)
else:
return e
J’effectue ici un premier test, histoire de savoir si les deux listes ont la même dimension.
>>> X.esp()
4.2Notez la présence de la division par l’effectif total.
J’ai souhaité en effet conserver cette division pour pouvoir effectuer des calculs sur les séries statistiques.
” e /= sum(self.P) “
Calcul de la variance
Je m’appuie sur le fait que \(V(X) = E[ (X-E(X))^2 ]\).
def var(self, r = None):
if (len(self.X) != len(self.P)) or sum(self.P) != 1.:
return False
m = self.esp()
V = [ ( self.X[i] - m )**2 for i in range( len(self.X) ) ]
Y = variable( V , self.P )
return Y.esp(r)
>>> X.var()
7.680000000000001Calcul de l’écart-type
def ecart(self , r = None):
if r != None:
return round(self.var()**0.5,r)
else:
return self.var()**0.5
>>> X.ecart(3)
2.771Calcul de la médiane
def mediane(self):
if (len(self.X) != len(self.P)):
return False
total = 0
for i in range( len(self.X) ):
total += self.P[i]
if total > sum(self.P)/2:
return self.X[i]
elif total == sum(self.P)/2:
return ( self.X[i] + self.X[i+1] ) / 2
>>> X.mediane()
4Cas d’une série statistique
Le dernier objet a été pensé pour pouvoir effectuer les calculs similaires sur des séries statistiques.
>>> L = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> N = [12, 23, 12, 45, 10, 13, 21, 31, 25, 17, 19]
>>> X.esp() # donne la moyenne de la série
5.144736842105263
>>> X.ecart()
3.019108503982276
>>> X.mediane()
5Le module
Téléchargement
Installation et utilisation
Vous pouvez installer ce fichier dans le répertoire courant de votre fichier principal Python, puis y faire appel:
# fichier principal Python
from probastat import binom
X = binom(50,0.11)
X.distrib('cyan','blue')
print( X.fluctuations().tableau )
print( X.fluctuations().intervalle )
Aide
>>> help(binom)
Help on class binom in module probastat:
class binom(builtins.object)
| binom(n, p)
|
| Objet 'binom'
| Déclaration : X = binom(n,p)
| Méthodes:
| * X.esp(<r>)
| * X.var(<r>)
| * X.ecart(<r>)
| * X.proba(k,<r>) -> retourne P(X = k)
| * X.proba_cdf(k,<r>) -> retourne P(X ≤ k)
| * X.proba_icdf(p) -> retourne la plus grande valeur de h telle que P(X ≤ h) ≤ p
| * X.simul(k, <couleur fond>, <couleur bord>) -> effectue k simulations et affiche le diagramme en barre
| * X.distrib( <couleur fond>, <couleur bord> ) -> distribution de X
| * X.fluctuations( <seuil = 0.95>) -> .tableau, .intervalle --> 'a' et 'b' tels que P(a ≤ X ≤ b) > seuil
|
| --> 'r' : nombre de chiffres après la virgule
|
| Methods defined here:
|
| __init__(self, n, p)
| Initialize self. See help(type(self)) for accurate signature.
|
| distrib(self, c=None, e=None)
|
| ecart(self, r=None)
|
| esp(self, r=None)
|
| fluctuations(self, seuil=0.95)
|
| proba(self, k, r=None)
|
| proba_cdf(self, k, r=None)
|
| proba_icdf(self, pr)
|
| simul(self, k, c=None, e=None)
|
| var(self, r=None)
|
| ----------------------------------------------------------------------
| Data descriptors defined here:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)>>> help(variable)
Help on class variable in module probastat:
class variable(builtins.object)
| variable(X, P)
|
| Objet 'variable'
| Déclaration : X = variable(liste valeurs , liste effectifs ou probabilités)
| Méthodes:
| * X.esp(<r>)
| * X.var(<r>)
| * X.ecart(<r>)
| * X.mediane(k,<r>) -> retourne P(X = k)
|
| --> 'r' : nombre de chiffres après la virgule
|
| Methods defined here:
|
| __init__(self, X, P)
| Initialize self. See help(type(self)) for accurate signature.
|
| ecart(self, r=None)
|
| esp(self, r=None)
|
| mediane(self)
|
| var(self, r=None)
|
| ----------------------------------------------------------------------
| Data descriptors defined here:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)

