Je me suis aujourd’hui penché sur les nombres premiers dont la somme des chiffres est première.

J’avais envie en effet, par curiosité, de regarder les nombres premiers pour lesquels la somme des chiffres était elle-même un nombre premier.

nombres premiers dont la somme des chiffres est première: introduction

J’ai commencé par regardé sur le moteur de recherche que j’utilise ce qui s’affichait quand je tape les mots « somme des chiffres des nombres premiers ». Je suis alors tombé sur cette page où l’on parle bien de la somme des chiffres des nombres premiers, mais où l’on insiste essentiellement sur sa parité.

Deux résultats intéressants sur les nombres premiers

Soit-dit en passant, je ne connaissais pas ce résultat:

Il y a en moyenne autant de nombres premiers dont la somme des chiffres décimaux est paire que de nombres premiers pour lesquels elle est impaire.

Hypothèse formulée en 1968 qui a été démontrée par des chercheurs de l’Institut de mathématiques de Luminy en 2010.

Il a tout de même fallu que j’aille sur le site de techno-sciences.net pour y voir plus clair.

Par là même, j’ai aussi appris (mieux vaut tard que jamais) le résultat suivant:

Tout nombre premier est de la forme 4k ± 1, où k est un entier naturel.

Tout nombre premier est de la forme 6k ± 1, où k est un entier naturel.

Démonstrations

Les démonstrations ne sont pas si difficiles que ça.

• Démonstration du premier résultat: tout nombre entier N peut s’écrire sous la forme 4k + r, avec 0 ≤ r < 4. Si N=4k, il n’est pas premier puisque divisible par 4. Si N = 4k+2 non plus car divisible par 2. Il ne reste que les cas où N=4k+1 et N=4k+3=4(k+1)-1=4K-1 qui peuvent éventuellement donner un nombre premier.
• Démonstration du second résultat: tout nombre entier N peut s’écrire sous la forme 6k + r, avec 0 ≤ r < 6. Si N=6k, ou N=6k+2 ou N=6k+3 ou N=6k+4 alors N est respectivement divisible par 4, 2, 3 et 2. Donc N n’est pas premier. Il ne reste que les cas où N=6k+1 et N=6k+5=6(k+1)-1=6K-1 qui peuvent éventuellement donner un nombre premier.

Je continuai donc mes recherches et tombai sur cette page, toujours du même site: celui de Gérard Villemin. Le problème est que je trouve la rédaction de ses pages très peu fluide et je n’y comprends rien au premier coup d’œil.

N’étant pas satisfait ce mes recherches, je continuai de mon côté.

nombres premiers dont la somme des chiffres est première: recherche à l’aide de Python

Je voulais déjà parcourir la liste des nombres premiers et voir si la somme des nombres était aussi première.

J’utilisai alors le programme suivant:

def is_prime(n):
    i = 2
    while i <= n**0.5:
        if n%i == 0:
            return False
        i += 1
    return True

def somme(n):
    n = list( str(n) )
    N = [int(k) for k in n]
    return sum( N )

if __name__ == '__main__':
    P = [ k for k in range(2,1000) if is_prime(k) ]
    for k in P:
        if somme(k) in P:
            print('{:3} : somme = {}'.format(k,somme(k)))

  2 : somme = 2
  3 : somme = 3
  5 : somme = 5
  7 : somme = 7
 11 : somme = 2
 23 : somme = 5
 29 : somme = 11
 41 : somme = 5
 43 : somme = 7
 47 : somme = 11
 61 : somme = 7
 67 : somme = 13
 83 : somme = 11
 89 : somme = 17
101 : somme = 2
113 : somme = 5
131 : somme = 5
137 : somme = 11
139 : somme = 13
151 : somme = 7
157 : somme = 13
173 : somme = 11
179 : somme = 17
191 : somme = 11
193 : somme = 13
197 : somme = 17
199 : somme = 19
223 : somme = 7
227 : somme = 11
229 : somme = 13
241 : somme = 7
263 : somme = 11
269 : somme = 17
281 : somme = 11
283 : somme = 13
311 : somme = 5
313 : somme = 7
317 : somme = 11
331 : somme = 7
337 : somme = 13
353 : somme = 11
359 : somme = 17
373 : somme = 13
379 : somme = 19
397 : somme = 19
401 : somme = 5
409 : somme = 13
421 : somme = 7
443 : somme = 11
449 : somme = 17
461 : somme = 11
463 : somme = 13
467 : somme = 17
487 : somme = 19
557 : somme = 17
571 : somme = 13
577 : somme = 19
593 : somme = 17
599 : somme = 23
601 : somme = 7
607 : somme = 13
641 : somme = 11
643 : somme = 13
647 : somme = 17
661 : somme = 13
683 : somme = 17
719 : somme = 17
733 : somme = 13
739 : somme = 19
751 : somme = 13
757 : somme = 19
773 : somme = 17
797 : somme = 23
809 : somme = 17
821 : somme = 11
823 : somme = 13
827 : somme = 17
829 : somme = 19
863 : somme = 17
881 : somme = 17
883 : somme = 19
887 : somme = 23
911 : somme = 11
919 : somme = 19
937 : somme = 19
953 : somme = 17
971 : somme = 17
977 : somme = 23
991 : somme = 19

Je remarquai alors que « 17 » et « 19 » apparaissaient assez souvent. Je décidai alors de modifier le programme afin de me donner les fréquences d’apparition des sommes possibles.

Voilà ce que j’obtins:

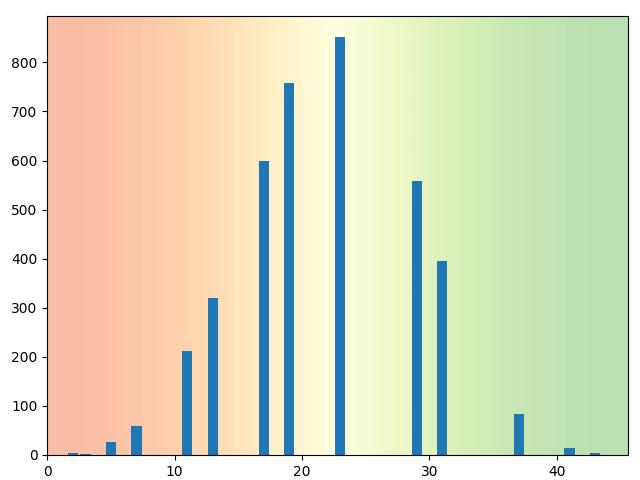
Je l’obtins à l’aide du dictionnaire engendré:

{2: 3, 3: 1, 5: 27, 7: 58, 11: 211, 13: 320, 17: 599, 19: 758, 23: 852, 29: 558, 31: 395, 37: 84, 41: 13, 43: 4}

Cette distribution me dit quelque chose… Pas vous ?

La somme moyenne est, après calcul, égale à 21,49163018284831.

Une autre simulation avec 50 000 nombres premiers

Plutôt que de prendre les nombres premiers jusqu’à 10 000, je suis allé jusqu’à 50 000:

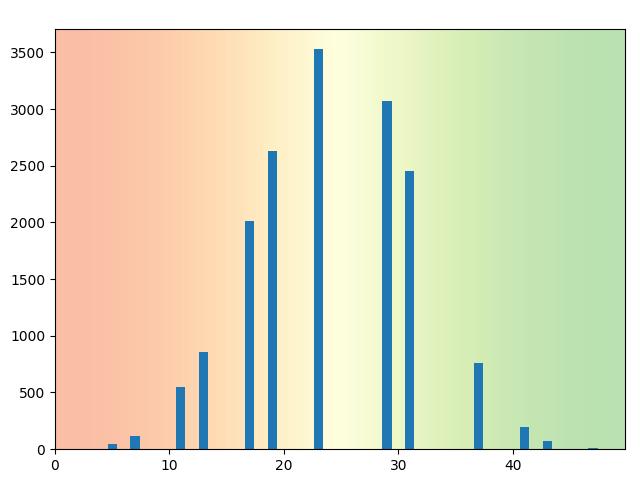
{2: 3, 3: 1, 5: 41, 7: 115, 11: 548, 13: 857, 17: 2010, 19: 2632, 23: 3533, 29: 3071, 31: 2453, 37: 760, 41: 197, 43: 73, 47: 7}

Somme moyenne : 23.826268327096496.

Une autre simulation avec 100 000 nombres premiers

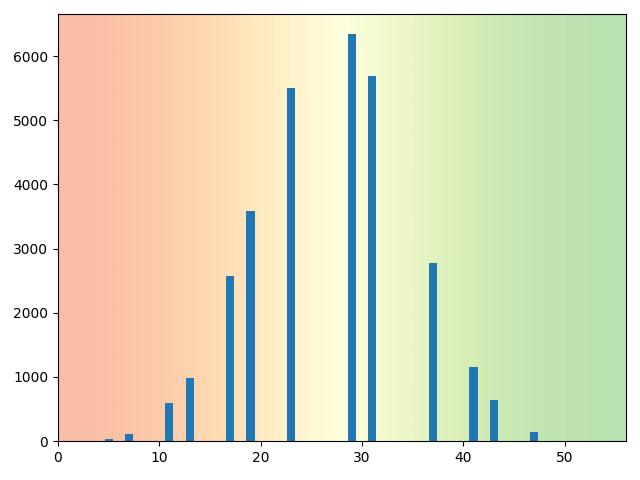
{2: 3, 3: 1, 5: 41, 7: 116, 11: 600, 13: 980, 17: 2570, 19: 3590, 23: 5503, 29: 6343, 31: 5682, 37: 2771, 41: 1148, 43: 634, 47: 140, 53: 1}

Somme moyenne : 26.63791787006606.

Épilogue

A priori, plus on augmente le nombre de nombres premiers dont la somme est elle-même un nombre premier, plus la somme moyenne grandit. Rien d’anormal au final… La distribution semble toujours être la même, seuls les paramètres changent (moyenne et variance).

Peut-être serait-il intéressant de voir si on peut corréler le nombre de nombres premiers pris et la somme moyenne des chiffres…

Il y aurait sans doute d’autres questions à se poser… Mais il est temps pour moi de revenir à la vraie vie 🙂

Les abonné·e·s à mathweb.fr trouveront ci-dessous le programme Python complet.