Vous connaissez sûrement les suites arithmétiques. Mais savez-vous qu’elles font partie d’une plus grande famille ?
Suites arithmétiques de degré d: introduction
La suite des carrés parfaits
Nous allons prendre l’exemple de la suite des carrés parfaits:$$u_n=n^2$$.
| Valeurs de n | Valeurs de n² |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
Maintenant, regardons la suite définie pour tout entier naturel n par:$$v_n=u_{n+1}-u_{n}.$$
| Valeurs de n | Valeurs de n² | Valeurs de \(v_n\) |
|---|---|---|
| 0 | 0 | – |
| 1 | 1 | \(v_0 = 1 – 0 = 1\) |
| 2 | 4 | \( v_1=4 – 1 = 3\) |
| 3 | 9 | \(v_2=9 – 4 = 5\) |
| 4 | 16 | \( v_3=16 – 9 = 7\) |
| 5 | 25 | \(v_4=25 – 16 = 9\) |
| 6 | 36 | \(v_5=36 – 25 = 11\) |
| 7 | 49 | \(v_6=49 – 36 = 13\) |
| 8 | 64 | \(v_7=64 – 49 = 15\) |
| 9 | 81 | \(v_8=81 – 64 = 17\) |
La suite \( (v_n) \) est arithmétique de raison r = 2.
On dira alors que \( (u_n) \) est une suite arithmétique de degré 2.
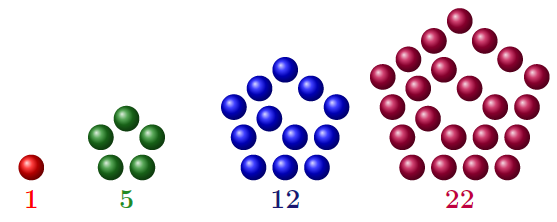
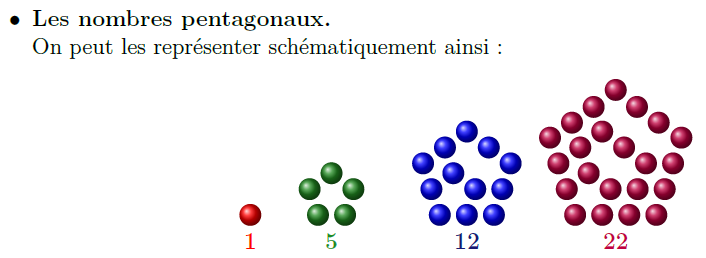
La suite des nombres pentagonaux
On peut représenter cette suite \( (u_n^{(0)}) \) ainsi:
On peut « décomposer » cette suite ainsi:
| Valeurs de \(u_n^{(0)}\) | \(u_n^{(1)} = u_n^{(0)} – u_{n-1}^{(0)}\) | \(u_n^{(2)} = u_n^{(1)}-u_{n-1}^{(1)}\) |
|---|---|---|
| \(u_0=1\) | ||
| \(u_1=5\) | 4 | |
| \(u_2=12\) | 7 | 3 |
| \(u_3=22\) | 10 | 3 |
| \(u_4=35\) | 13 | 3 |
Cette suite est aussi une suite arithmétique de degré 2. Dans ce tableau , j’ai volontairement « poussé » jusqu’à obtenir une suite constante pour mettre en relief la raison pour laquelle le degré est 2: on a « décomposé » la suite initiale à l’aide de 2 suites, dont la dernière est constante.
Suites arithmétiques de degré d: généralités
Définition d’une suite arithmétique de degré d
Une suite numérique \( (u_n^{(0)}) \) est arithmétique de degré d s’il existe un ensemble de suites \( \{ (u_n^{(1)}) \}, \{ (u_n^{(2)}) \}, …, \{ (u_n^{(d)}) \} \) telles que:$$\forall p \in [0 ; d-1]\cap\mathbb{N},\ \forall n\in\mathbb{N}^*,\ u_n^{(p)} = u_{n-1}^{(p)}+u_{n-1}^{(p+1)}\,,$$ où \( (u_n^{(d)}) \) est une suite constante.
La raison d’une telle suite est la valeur de \( u_0^{(d)} \).
Un autre exemple
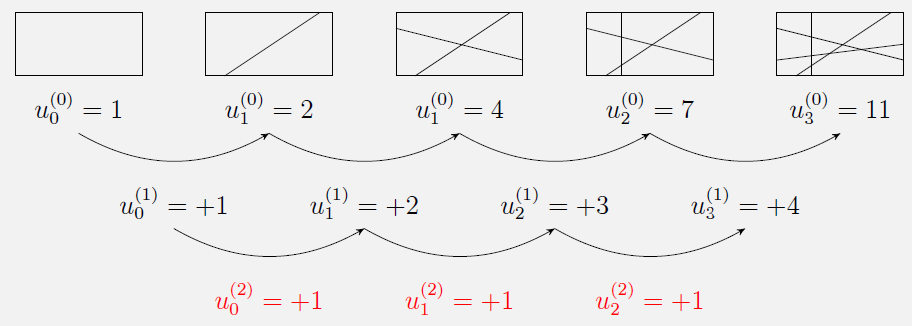
Si on découpe un plan à l’aide de n droites, le nombre maximum de régions du plan est une suite arithmétique de degré 2 et de raison 1.
Terme général d’une suite arithmétique de degré d
Si \( (u_n^{(d)}) \) est une suite arithmétique de degré d et de raison r, alors:$$\forall n\in\mathbb{N},\ u_n^{(0)} = \sum_{m=0}^{d-1}\left(u_0^{(m)}P_m(n)\right)+rP_d(n)\,,$$où la famille de polynômes \(P_k(n)\) est définie par:$$\forall n\in\mathbb{N},\ \begin{cases} P_0(n)=1\\\forall k\in\mathbb{N},\ P_{k+1}(n)=\displaystyle\sum_{j=1}^nP_k(j) \end{cases}$$
La démonstration est plutôt longue mais elle est disponible dans mon livre « Ainsi de suite« , disponible gratuitement en téléchargement au format PDF. Cela se démontre par récurrence.
Conséquences
Ce dernier résultat montre que le terme général d’une suite arithmétique de degré d s’exprime comme un polynôme de degré d:$$\forall\ n\in\mathbb{N},\ u_n^{(d)} = \alpha_dn^d + \cdots + \alpha_1n + \alpha_0.$$ Pour déterminer la valeur des coefficients \(\alpha
_k\), il suffit de résoudre le système linéaire de Vandermonde suivant :$$\begin{cases}u_1^{(0)} & = & \alpha_0 + \alpha_1 + \cdots + \alpha_d\\u_2^{(0)} & = & \alpha_0 + 2\alpha_1 + \cdots + 2^d\alpha_d\\\vdots & & \\u_{d+1}^{(0)} & = & \alpha_0 + (d+1)\alpha_1 + \cdots + (d+1)^d\alpha_d\end{cases} $$
Une application aux suites arithmétiques de degré d: les nombres polygonaux
Nous en avons brièvement parlé précédemment lorsque nous avons regardé la suite pentagonale.
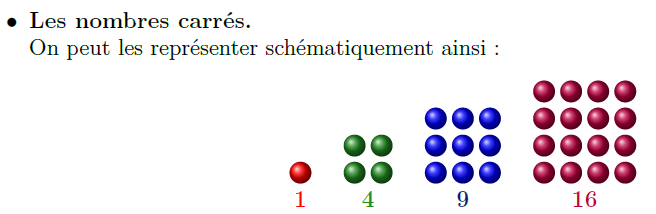
On arrive à démontrer à l’aide du résultat précédent que:$$\forall\; p\geqslant 3,\ u_n^{(p)} = \frac{n\left(4-p+(p-2)n\right)}{2}.$$
Un peu de Python
Je vous propose un programme Python qui permet de voir si une suite est arithmétique de degré d.
def is_ardeg(liste , degre = 0):
if len(liste) != 1:
comp = [0] * len(liste)
if liste == comp:
return True , degre-1
else:
# on vérifie s'il y a deux éléments identiques dans la liste
comp = [ liste[0] ] * len(liste)
if liste != comp:
for e in liste:
i = liste.index(e)
L = liste[:i] + liste[i+1:]
if e in L:
return False
u = []
for n in range(1,len(liste)):
u.append( liste[n-1] - liste[n] )
return is_ardeg(u,degre+1)
else:
return False , "Pas assez d'éléments pour conclure.">>> L = [i**2 for i in range(10)]
>>> is_ardeg(L)
(True, 2)
>>> is_ardeg([1, 3, 5, 7, 8, 9, 11])
False