Intéressons-nous à un problème faisant intervenir les permutations dans lequel il nous est demandé de déterminer la somme des résultats.
Permutations et somme des résultats: l’énoncé du problème
Le problème sur lequel nous allons nous pencher est exposé dans cette vidéo. Je vais l’aborder différemment… et en français 🙂
Soit S l’ensemble des nombres à 5 chiffres formés en utilisant les chiffres 1, 2, 3, 4, 5 sans répétition. Quelle est la somme de tous les éléments de S ?
Permutations et somme des résultats: première approche mathématique
Il s’agit avant tout de savoir comment est constitué l’ensemble S. Pour les connaisseurs, il s’agit bien évidemment d’une permutation de l’ensemble {1,2,3,4,5}. Il y a donc 5! = 120 éléments dans S.
Pour les non initiés, je vais tenter de vous expliquer la logique: commençons par un ensemble {1,2,3} et trouvons toutes les permutations de cet ensemble, c’est-à-dire tous les nombres à 3 chiffres composés des chiffres 1, 2 et 3 sans que ceux-ci se répètent. On peut les énumérer facilement:
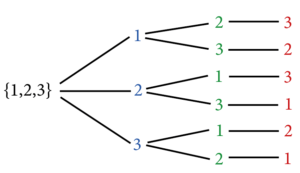
- ceux commençant par « 1 » : on a alors le choix entre les nombres « 2 » et « 3 » pour le deuxième chiffre, et il ne restera alors qu’un choix pour le dernier chiffre;
- ceux commençant par « 2 »: on a alors le choix entre les nombres « 1 » et « 3 » pour le deuxième chiffre, et il ne restera alors qu’un choix pour le dernier chiffre;
- ceux commençant par « 3 »: on a alors le choix entre les nombres « 1 » et « 2 » pour le deuxième chiffre, et il ne restera alors qu’un choix pour le dernier chiffre.
On peut visualiser ces choix à l’aide d’une représentation graphique, que l’on appelle arbre des possibilités.
On voit qu’il y a 3 choix pour le premier chiffre, 2 pour le deuxième et 1 pour le dernier; le nombre de permutations est donc: \(3\times2\times1=6\). On note cela aussi: \(6! = 3\times2\times1\).
Si on généralise ceci à l’ensemble {1,2,3,4,5}, on trouve qu’il y a \(5!=5\times4\times3\times2\times1=120\) permutations.
Les permutations font partie d’une branche des mathématiques que l’on appelle la combinatoire. C’est la même logique que les anagrammes.
Permutations et somme des résultats: approche en Python du problème
En Python, il existe le module itertools qui nous permet de construire les permutations de l’ensemble {1,2,3,4,5}. Il retourne les résultats sous la forme de 5-uples, qu’il nous faudra transformer en nombres afin de pouvoir en faire la somme. Pour cela, je vais utiliser la fonction map.
from itertools import permutations
S = 0 # somme initiale: on part de zéro
for i in permutations([1,2,3,4,5]):
S += int( ''.join( map(str,i) ) )
print( S )Explications:
- d’abord, on parcourt toutes les permutations de l’ensemble {1, 2, 3, 4, 5} (mis pour l’occasion sous forme de liste) : c’est la boucle de la ligne 5;
- « map(str,i) » transforme l’item i (donc une permutation sous la forme d’un 5-uple) en une liste de caractères;
- « join( map(str,i) ) » transforme la liste de caractères en chaîne de caractères;
- int( ».join( map(str,i) ) ) transforme la chaîne de caractères en nombre entier
- « S += int( ».join( map(str,i) ) ) » est une autre syntaxe que « S = S + int( ».join( map(str,i) ) ) » : on ajoute à ce qui était dans la variable S l’entier obtenu
S représente alors la somme de toutes les permutations.
On trouve alors qu’l y en a 3 999 960.
Approche en mathématique du problème
Quand un problème est complexe, j’ai souvent l’habitude de le simplifier au maximum pour en comprendre les rouages, et c’est ce que nous allons faire à travers le premier exemple (permutation de l’ensemble {1,2,3}).
Les nombres obtenus par permutations de {1,2,3} constituent un ensemble S et sont de la forme:$$\overline{x_2x_1x_0}=100x_2+10x_1+x_0.$$ Par exemple,$$123=100\times1+10\times2+3.$$On cherche donc à ajouter tous ces nombres:$$\sum_{S}100x_2+10x_1+x_0=100\sum_{S}x_2+10\sum_{S}x_1+\sum_{S}x_0.$$Or, $$\sum_{S}x_2=\sum_{S}x_1=\sum_{S}x_0$$car tous les chiffres apparaissent un même nombre de fois pour chacune des positions dans le nombre. La somme vaut donc:$$(100+10+1)\sum_{S}x_0=111\sum_{S}x_0.$$De plus,$$\sum_{S}x_0=2\times(1+2+3)=12$$car chaque chiffre apparaît ici deux fois.
La somme cherchée sur notre exemple est donc:$$111\times12=1332.$$
Revenons maintenant à la somme des permutations de {1,2,3,4,5}. Avec les mêmes notations que précédemment, on obtient que la somme est:$$(10^5+10^4+10^3+10^2+10+1)\sum_{S}x_0=11111\sum_{S}x_0.$$Il nous faut maintenant trouver combien chaque chiffre apparaît à une position donnée. Il suffit de compter combien de « 1 » apparaissent en première position par exemple: combien de permutations commencent par « 1 » sachant qu’il reste 4 chiffres? Il y en a 4!=24.
Maintenant, on calcule la somme:$$5+4+3+2+1=15.$$La somme de toutes les permutations est alors:$$11111\times15\times24=3999960.$$Le compte est bon!
Généralisation
Quelle est la somme de toutes les permutations de l’ensemble {1,2,3,…,n} ?
D’après ce qui a été vu précédemment, on peut dire que cette somme est:$$\left(\sum_{k=0}^n10^k\right) \times \left(\sum_{k=1}^n k\right) \times (n-1)!.$$