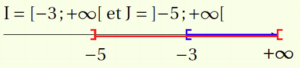Quand on enseigne l’union et l’intersection d’intervalles en classe de Seconde, on est souvent amené à dessiner sur l’axe des réels ces intervalles. C’est assez pénible à faire quand on en a une sacrée dose…
C’est ce que j’ai pu constater quand j’ai voulu aujourd’hui proposer un exercice avec douze questions. Pour chacune d’elles, il fallait dessiner les deux intervalles pour visualiser leur union et leur intersection (avec \(\LaTeX\)).
Bien que cela m’ait prix énormément de temps, j’ai réalisé un script Python qui permet de générer les graphiques à la chaîne à partir des questions.
Union et intersection d’intervalles en Seconde: le script Python
En \(\LaTeX\), j’ai 12 questions formatées ainsi:
\item $I=\intervOF{-3}{7}$ et $J=\intervFO{-1}{+\infty}$
\item $I=\intervOO{-\infty}{4}$ et $J=\intervFF{4}{10}$
\item $I=\intervFF{-10}{2}$ et $J=\intervFF{-3}{7}$
\item $I=\intervOF{-\infty}{3}$ et $J=\intervFO{-6}{+\infty}$
\item $I=\intervFO{7}{+\infty}$ et $J=\intervFO{-5}{+\infty}$
\item $I=\intervOF{3}{18}$ et $J=\intervOF{17}{20}$
\item $I=\intervFF{-3}{0}$ et $J=\intervFO{-1}{+\infty}$
\item $I=\intervFO{-2}{0}$ et $J=\intervFO{0}{+\infty}$
\item $I=\intervOO{7}{18}$ et $J=\intervFO{10}{+\infty}$
\item $I=\intervOO{-4}{2}$ et $J=\intervFF{2}{5}$
\item $I=\intervOO{-4}{2}$ et $J=\intervOF{2}{5}$
\item $I=\intervFO{-3}{+\infty}$ et $J=\intervOO{-5}{+\infty}$Ce que je voulais, c’est prendre chacune de ces lignes et construire l’axe des réels sur lequel seraient dessinés les deux intervalles, de deux couleurs différentes (mais en fait, le script fonctionne pour plus de deux intervalles).
Alors, comme expliquer un code est super méga pénible, je vais plutôt vous montrer ce que j’ai fait:
import re
def CG(x): # crochet vers la gauche
return f"\\draw[thick] ({x-0.1},0.1) -- ({x},0.1) -- ({x},-0.1) -- ({x-0.1},-0.1);\n"
def CD(x): # crochet vers la droite
return f"\\draw[thick] ({x+0.1},0.1) -- ({x},0.1) -- ({x},-0.1) -- ({x+0.1},-0.1);\n"
tex = """\item $I=\intervOF{-3}{7}$ et $J=\intervFO{-1}{+\infty}$
\item $I=\intervOO{-\infty}{4}$ et $J=\intervFF{4}{10}$
\item $I=\intervFF{-10}{2}$ et $J=\intervFF{-3}{7}$
\item $I=\intervOF{-\infty}{3}$ et $J=\intervFO{-6}{+\infty}$
\item $I=\intervFO{7}{+\infty}$ et $J=\intervFO{-5}{+\infty}$
\item $I=\intervOF{3}{18}$ et $J=\intervOF{17}{20}$
\item $I=\intervFF{-3}{0}$ et $J=\intervFO{-1}{+\infty}$
\item $I=\intervFO{-2}{0}$ et $J=\intervFO{0}{+\infty}$
\item $I=\intervOO{7}{18}$ et $J=\intervFO{10}{+\infty}$
\item $I=\intervOO{-4}{2}$ et $J=\intervFF{2}{5}$
\item $I=\intervOO{-4}{2}$ et $J=\intervOF{2}{5}$
\item $I=\intervFO{-3}{+\infty}$ et $J=\intervOO{-5}{+\infty}$
"""
L = [ 'intervOO', 'intervFF' , 'intervFO' , 'intervOF' ]
couleurs = [ 'blue' , 'red' ]
latex = '\\begin{enumerate}\n'
for line in tex.split('\n'):
if line != '':
latex += line + '\n\n'
R = re.findall("{(.+?)}",line) # R = [ a, b, c, d]
I = sorted( [ (line.find(i),L.index(i)) for i in L if line.find(i) != -1] )
if len(I) == 1:
I.append( (I[0][0]+1,I[0][1]) )
#minimum et maximum pour la droite des réels
RR = [ int(i) for i in R if i != '+\\infty' and i != '-\\infty' ]
minTiKZ, maxTiKZ = min(RR)-2, max(RR)+2
if maxTiKZ-minTiKZ > 15:
scale = 15/(maxTiKZ-minTiKZ)
else:
scale = 1
latex += "\\begin{tikzpicture}[scale="+str(scale)+", every node/.style={scale="+str(scale)+"}]\n"
latex += f"\\draw[->,>=latex] ( {minTiKZ},0) -- ({maxTiKZ},0);\n"
n = 0
for i in I:
latex += "\\begin{scope}[draw="+couleurs[I.index(i)]+"]\n"
# on trace le segment
a, b = R[0+n], R[1+n]
if R[0+n] == "-\\infty":
a = minTiKZ
na = "$-\\infty$"
else:
a = R[0+n]
na = f'${a}$'
if R[1+n] == "+\\infty":
b = maxTiKZ
nb = "$+\\infty$"
else:
b = R[1+n]
nb = f'${b}$'
if n == 0:
latex += f"\\draw[thick] ({a},0) -- ({b},0);\n"
else:
latex += f"\\draw[thick] ({a},-0.03) -- ({b},-0.03);\n"
# on trace les crochets
match i[1]:
case 0: latex += CG(float(a)) + CD(float(b))
case 1: latex += CD(float(a)) + CG(float(b))
case 2: latex += CD(float(a)) + CD(float(b))
case _: latex += CG(float(a)) + CG(float(b))
latex += "\\node[below,inner sep=3mm] at ("+str(a)+",0) {"+na+"};\n"
latex += "\\node[below,inner sep=3mm] at ("+str(b)+",0) {"+nb+"};\n"
latex += "\\end{scope}\n"
n += 2
latex += "\\end{tikzpicture}\n"
latex += "\\end{enumerate}"
print( latex )Ouais, il est pas très court… Mais ça, c’est parce que je suis sans doute trop nul avec les expressions régulières! Je me suis sans doute bien compliqué la vie à ce niveau… Mais bon! Quand on est nul, il faut faire avec notre ignorance… 🙂
Quoi qu’il en soit, après plusieurs heures, j’ai enfin réussi à produire quelque chose qui fonctionne. Cerise sur le gâteau: quand la droite dépasse 15 cm, la droite des réels est réduite. Bon, on peut ajouter et mettre autre chose que 15cm, rassurez-vous!
Bon, sans plus attendre (parce que je vous connaît les petits coquinoux: vous avez envie de voir ce que ça donne), voici quelques captures:
En fait, le script Python ne fait que générer un code \(\LaTeX\) sous la forme:
\begin{enumerate}
\item La question
\begin{tikzpicture}
le code dessinant l'axe et les intervalles
\end{tikzpicture}Et non! Il ne résout pas tout seul la question: il faut tout de même se taper à la main les solutions… Z’avez cru quoi non mais ?! 🙂
Explications succinctes sur les contraintes
Concernant le formatage des questions, celui qui va passer à la moulinette Python, il faut juste respecter une chose: utiliser la syntaxe suivante pour écrire les intervalles.
\intervFF{a}{b} % [a,b]
\intervOO{a}[b} % ]a,b[
\intervFO{a}{b} % [a,b[
\intervOF{a}{b} % ]a,b]Cette syntaxe est issue de mon package \(\LateX\) pas-math. Ce package permet d’écrire des choses mathématiques de façon peut-être plus simple (comme les intervalles justement).
Après, concernant la syntaxe de la question en elle-même, du moment qu’il y a plusieurs intervalles, le code comprend… Vous pouvez même mettre:
\item \intervOO{5}{13} et \intervOF{-2}{7}N’hésitez pas à me dire si je suis un gros nullos et que vous avez plus simple comme code (bon, mettez-y les formes quand-même hein ? Il ne s’agirait pas de trop me vexer… 🙂 ) Laissez un commentaire en bas de page dans ce cas!