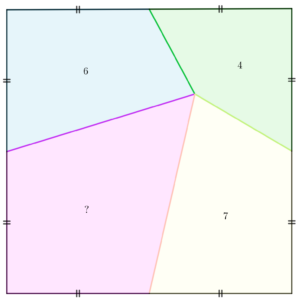
Il y a quelques temps, j’ai vu le problème mathématique d’aire suivant: étant donnée la figure suivante, trouver l’aire manquante.

Problème mathématique d’aire: première approche

Je vais noter \(c\) la mesure du carré. Ainsi, la somme des quatre aires est égale à \( c^2\), donc:$$c^2=17+x\quad\text{soit}\quad c=\sqrt{17+x}.$$ On peut raisonnablement accepter le fait que l’aire du carré ne dépasse pas 36, et donc que \(c\) ne soit pas plus grand que 6. Mais la donnée de cette fonction de \(x\) ne nous avance pas trop…

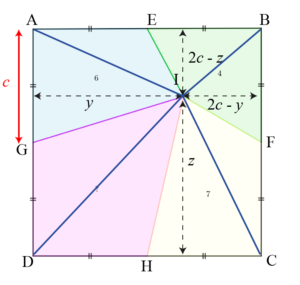
Problème mathématique d’aire: une approche plus algébrique

Cette fois-ci, je vais noter \(c\) la mesure de la moitié d’un côté du carré, et je vais introduire des variables \(y\) et \(z\) comme indiqué ci-dessous sur la figure:

Problème mathématique: Aire de AEIG

C’est la somme de l’aire des triangles AEI et AIG:$$\mathcal{A}_1=\frac{1}{2}c(2c-z) + \frac{2}{2}cy = \frac{1}{2}c(2c-z+y)=6.$$

Aire de EBFI

C’est la somme de l’aire des triangles EBI et BIF:$$\mathcal{A}_2=\frac{1}{2}c(2c-z+2c-y) = \frac{1}{2}c(4c-z-y)=4.$$

Aire de HCFI

C’est la somme de l’aire des triangles CFI et HCI:$$\mathcal{A}_3=\frac{1}{2}c(2c-y+z)=7.$$

Aire de GDHI

C’est la somme de l’aire des triangles GDI et DHI:$$\mathcal{A_4}=\frac{1}{2}c(y+z)=x.$$

Égalités

De tout ceci, on en déduit notamment les égalités:$$\begin{cases}c(2c-z)=12\\c(4c-z-y)=8\\c(2c-y+z)=14\\c(y+z)=2x\end{cases}$$Des deuxième et quatrième égalités, on déduit:$$c(4c-(y+z))=8 \iff 4c^2-2x=8 \iff x = 2c^2-4.$$

Comme nous l’avons mentionné plus haut, on peut raisonnablement penser que \( 6 < x < 36\) d’où:$$\begin{align}6 < 2c^2-4 < 36 & \iff 3 < c^2-2 < 18\\ & \iff 5 < c^2 < 20\\&\iff \sqrt3 < c < 2\sqrt5 \end{align}$$

Conclusion

On sait que:$$\begin{cases}x = 2c^2-4\\4c^2=17+x\end{cases}$$et donc:$$2c^2-4=4x^2-17 \iff 2c^2=13.$$

On en déduit alors que:$$x=9.$$