J’avais envie de construire un solide particulier en m’appuyant sur une courbe aux caractéristiques bien précises… Voici le résultat:
Construire un solide particulier: les contraintes
Je voulais avant tout construire une courbe dans un repère du plan. La fonction \(f\) devait, dont la courbe devait être représentative, devait impérativement satisfaire les quatre conditions suivantes:
- \( f(x) = g(x)\text{e}^{-x} \)
- \( f(0) = 0 \)
- \( f(7) = 0 \)
- \( f'(0) = +\infty \)
Et si la fonction g était un polynôme ?
Au début, je cherche à faire simple et regarde si un polynôme conviendrait pour la fonction g… Mais très vite, je m’aperçois que ce n’est pas possible à cause de la contrainte sur la dérivée en 0.
En effet, la dérivée d’un polynôme est toujours un polynôme et donc son nombre dérivé en 0 ne peut pas être infini.
À la recherche de la fonction g
Suite à ce constat, je m’oriente vers une fonction qui pourrait avant tout satisfaire cette contrainte sur le nombre dérivé en 0. Il y a le choix entre une fonction inverse et un radical.
Le deuxième choix semble plus approprié quand on regarde la contrainte de l’image de 0 par la fonction f…
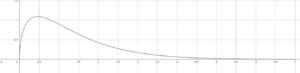
Je vais donc chercher une fonction g sous la forme \( g(x) = \sqrt{ax^2+bx} \) (pour satisfaire la contrainte \(f(0)=0\). Très rapidement, à l’aide de la contrainte \( f(7) = 0\), j’obtiens:$$ f(x) = \sqrt{x(7-x)}\text{e}^{-x}.$$
La courbe représentative de f est alors la suivante:
Construire un solide particulier: le volume
Si on engendre un solide à partir de cette courbe en la faisant tourner autour de l’axe des abscisses, on obtient ceci:
Je souhaite à présente calculer le volume de ce solide. Pour cela, je considère que le volume est la somme infinitésimale d’aires de disques de rayon \(f(x)\), pour \(x \in [0;7]\).
Le volume est donc:$$\mathcal{V} = \int_0^7 \pi \times \big[ f(x) \big]^2 \text{d}x = \pi\int_0^7 x(7-x)\text{e}^{-x}\text{d}x.$$;
Bon, là, un petit coup d’intégration par parties devrait faire l’affaire! J’explique ? Allez, j’explique. Je pose:$$\begin{array}{ll} u'(x)=\text{e}^{-x}\qquad & v(x)=-x^2+7x \\ u(x)=-\text{e}^{-x} & v'(x)=-2x+7 \end{array}$$On a alors:
$$\begin{align}\mathcal{v} & = \pi\int_0^7 u'(x)v(x) \text{d}x\\ & = \pi \big[ u(x)v(x) \big]_0^7 – \pi\int_0^7 u(x)v'(x)\text{d}x\\ & = \pi\big( (uv)(7) – (uv)(0) \big) – \pi\int_0^7 u(x)v'(x)\text{d}x\\ & = – \pi\int_0^7 u(x)v'(x)\text{d}x \\ & = \pi\int_0^7 (-2x+7)\text{e}^{-x}. \end{align}$$
Une deuxième intégration par parties s’impose en posant:$$\begin{array}{ll} u'(x)=\text{e}^{-x}\qquad & v(x)=-2x+7 \\ u(x)=-\text{e}^{-x} & v'(x)=-2 \end{array}$$
On obtient:$$\begin{align} \mathcal{V} & = \pi \big[ (uv)(7)-(uv)(0) \big] – \pi\int_0^7 u(x)v'(x)\text{d}x\\ & = \pi( 7\text{e}^{-7} + 7) +2 \pi\int_0^7 \text{e}^{-x}\text{d}x\\ & = \pi( 7\text{e}^{-7} + 7) -2 \pi\big[ -\text{e}^{-x} \big]_0^7 \\ & = \pi( 7\text{e}^{-7} + 7) -2 \pi\big( -\text{e}^{-7} + 1 \big)\\&=\big(9\text{e}^{-7}+5\big)\pi.\end{align}$$
Quid de la surface du solide?
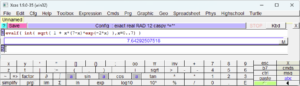
La surface du solide est obtenue en multipliant la longueur de la courbe sur [0;7] par \(2\pi\). La longueur d’une courbe est donnée par la formule:$$\mathcal{L}=\int_0^7 \sqrt{1+f(x)^2}\text{d}x = \int_0^7 \sqrt{1+x(7-x)\text{e}^{-2x}} \text{d}x.$$
Et là, c’est le drame… ! Fort heureusement, nous avons de bons outils pour en donner une approximation (nous ne sommes plus au Moyen-Âge!). J’utilise personnellement le logiciel Xcas.
Oui, parce que bon… Le calcul théorique de l’intégrale me semble bien compliqué…
En multipliant cette valeur par \(2\pi\), on arrive à une surface d’environ 48 unités d’aires.
Ainsi, si on décide de construire un tel objet, en prenant comme unité de longueur le centimètre, et si l’on souhaite le peindre, on saura qu’il faut environ 48 cm² de peinture.