Cet exercice, qui consiste à trouver la mesure d’un angle dans un triangle où l’on connait la mesure de deux côtés et celle d’un autre angle, a été proposé lors d’un test à des élève suisses, dont le niveau équivaut à celui de 1ère en France.
Je dois bien dire que cela m’a laissé perplexe au premier abord car ce n’était que la première question sur deux.
N’étant pas habitué au niveau d’exigence de l’enseignement suisse, je ne savais pas trop si la solution devait être « évidente » ou pas… Quoi qu’il en soit, pour moi, elle n’était pas immédiate!
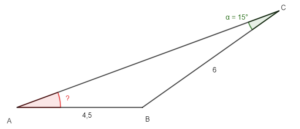
Comment trouver la mesure de l’angle manquant dans ce triangle?
La configuration proposée m’a fait pensé immédiatement au théorème d’Al-Kashi. Mais il me fallait en premier lieu calculer la mesure du côté AC… et pour cela, ce même théorème était aussi utilisable.
Trouver la mesure de l’angle dans le triangle: on commence par calculer AC
D’après le théorème d’Al-Kashi, on peut écrire:$$\begin{align}AB^2 & = CA^2+CB^2-2\times CA \times CB \times \cos(15^\circ)\\\iff 4,5^2 & = AC^2 + 6^2 – 12AC\cos(15^\circ)\\\iff & AC^2 – 12\cos(15^\circ)AC + 15,75=0\end{align}$$
\(AC\) est alors une des solutions de cette dernière équation du second degré, de discriminant:$$\begin{align}\Delta & =144\cos^2(15^\circ)-63\\ & = 144\times\left(\frac{\sqrt2+\sqrt6}{4}\right)^2-63\\&=36\sqrt3+9.\end{align}$$On trouve alors deux solutions à l’équation:$$\begin{align} x_1 & = \frac{12\cos(15^\circ)-\sqrt{ 36\sqrt3+9 }}{2} \\ & = \frac{3\big(\sqrt2+\sqrt6\big)-\sqrt{36\sqrt3+9}}{2} \\x_1 & \approx 1,57\end{align}$$et$$\begin{align}x_2 & = \frac{3\big(\sqrt2+\sqrt6\big)+\sqrt{36\sqrt3+9}}{2}\\ & \approx10,02.\end{align}$$
Il va de soit que seule la dernière valeur convient à notre problème. On a alors:$$AC \approx 10,02.$$
Trouver la mesure de l’angle demandé dans le triangle ABC
Maintenant que nous avons \(AC\), utilisons à nouveau le théorème d’Al-Kashi pour trouver l’angle demandé:$$\begin{align}BC^2 & = AB^2 + AC^2 – 2\times AB \times AC \times\cos(\widehat{A}) \\ \iff 36 & \approx 4,5^2 + 10,02^2 – 2\times4,5\times10,02\times\cos(\widehat{A}) \\ \iff \cos(\widehat{A}) & \approx 0,938682634731\\\iff \widehat{A} & \approx 20^\circ.\end{align}$$
Réflexions
Vous vous demandez peut-être pourquoi je m’embête à garder autant de valeurs exactes et autant de décimales jusqu’au résultat final, non ?
Si tel est le cas, je vous rassure: ce n’est pas parce que je suis fou… 🙂 mais parce que dès que nous donnons une valeur approchée « trop arrondie », le résultat final n’est pas celui attendu. Croyez-moi sur parole: j’ai essayé d’arrondir à plusieurs endroits, et je n’arrivais jamais exactement à 20 degrés, mais à 17 degrés par exemple. C’est dingue comme notre façon d’arrondir peut avoir une incidence majeure sur les calculs de mesures d’angles!
Si vous avez une solution plus simple, n’hésitez pas à la proposer en commentaire! Car à mon avis, il y a en effet plus simple…



Je calcule la hauteur issue de B:
Soit H le pied de B, \(\sin(\widehat{BCA}) = \frac{HB}{BC}\), donc \(HB=\sin(\widehat{BCA}) \times BC = 6 \sin(15^\circ). \)
De plus, \( \sin(\widehat{BAC}) = \frac{HB}{4,5} = \frac{6\sin(15^\circ)}{4,5} \approx 0,345. \)
Ainsi, \(\widehat{BAC} \approx 20^\circ \).
Je me demande pourquoi je n’ai pas eu cette idée, plutôt évidente au final… C’est une méthode tellement classique que l’on peut même voir au collège… Merci pour cette proposition!