Les tests faux positifs sont bien connus en probabilités. C’est une sorte de paradoxe contre-intuitif que beaucoup de personnes ont du mal à saisir. Même les médecins s’y trompent selon une étude de l’institut Max-Planck d’il y a pas mal d’années (je ne retrouve plus les sources malheureusement).
Tests faux positifs: introduction
J’ai parlé des médecins, mais le modèle du « faux-positif » peut s’appliquer dans d’autres domaines. Quand on effectue un test (biologique ou sociologique par exemple), il y a toujours une marge d’erreur. Un test de grossesse peut être positif alors que la femme n’est pas enceinte. C’est ce que l’on appelle le « faux-positif ».
Nous allons donc nous pencher sur ce problème. Quelle est la probabilité d’être réellement malade (par exemple) sachant que le test est positif ? Combien de tests doit-on faire pour être assuré(e)s d’être réellement malade au seuil de 95% (par exemple) ?
Avant toute chose, je précise que l’article de wikipedia concernant ces faux positifs peut vous apporter un autre angle.
Tests faux positifs: un exemple médical
L’énoncé
On a un test de sérologie pour identifier une maladie qui atteint 0,5% de la population.
Sur 99% des malades, le test réagit. Autrement dit, 99% des malades sont détectés par ce test. Mais sur 2% des personnes saines, le test montre une fausse réaction positive.
Sur un patient, un test est positif. Quelle est la probabilité d’être malade ?
Résolution du problème
Nous allons noter:
- « M » l’événement : « le patient est malade »
- « R » l’événement : « le test réagit »
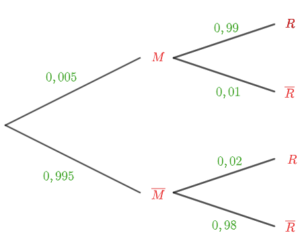
L’arbre des probabilités correspondant à notre situation est le suivant:
$$\begin{align*}P(R) & = P(M \cap R) + P(\overline{M}\cap R)\\ & = 0,005\times0,99+0,995\times0,02\\ & =0,02485.\end{align*}$$
On en déduit alors, d’après la formule de Bayes:$$\begin{align*}P_R(M) &= \frac{P_M(R)\times P(M)}{P(R)}\\& = \frac{P(M \cap R)}{P(R}\\& = \frac{0,005\times0,99}{0,02485}\\&\approx0,199.\end{align*}
On peut alors conclure que le patient est réellement malade avec une probabilité d’environ 20%… ce qui est peu!
Combien de tests au minimum pour être sûrs d’être malade ?
On ne peut jamais être sûrs à 100%, mais on peut se rapprocher de cette probabilité en multipliant les tests. Mais combien de tests au minimum afin que la probabilité atteigne au moins 95% ? Nous allons le calculer.
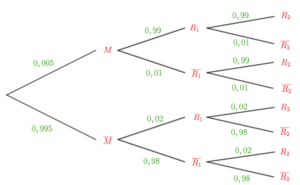
Pour commencer, faisons un autre test. L’arbre suivant décrit la situation:
On convenant de noter:
- \(R_1\) l’événement : « le premier test réagit »
- \(R_2\) l’événement : « le second test réagit »
Nous cherchons à calculer : $$\begin{align*}P_{(R_1\cap R_2)}(M) & = \frac{P(M \cap R_1 \cap R_2)}{P(R_1 \cap R_2)}\\ & = \frac{0,005 \times 0,99^2}{0,005\times0,99^2+0,995\times0,02^2} \\&\approx0,9249.\end{align*}$$
Nous voyons alors que deux tests suffisent pour assurer une probabilité d’au moins 90%. On constate alors la nécessité d’effectuer un deuxième.
Si on note n le nombre de tests, et A l’événement : « tous les tests réagissent », nous avons:$$\begin{align*}P_A(M) & = \frac{P(M \cap A)}{P(A)}\\ & = \frac{0,005\times0,99^n}{0,005\times0,99^n+0,995\times0,02^n} \end{align*}$$
On calcule alors que pour n = 3n cette probabilité atteint 99,8%.
Tests faux positifs: cas général
Une formule générale
Notons:
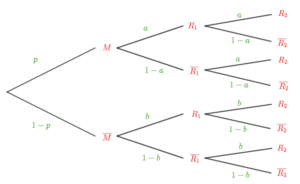
- n le nombre de tests effectués (sur le schéma ci-dessous, je me contente de prendre n = 2)
- p la probabilité d’être malade (ou de présenter une quelconque particularité)
- a la probabilité que le test soit positif sachant que la personne présente la particularité cherchée
- b la probabilité que le test soit un faux positif
- X la variable aléatoire représentant le nombre de tests positifs
On peut généraliser ce qui a été fait en amont:$$P_{(X=k)}(M) = \frac{p \times \binom{n}{k}\times a^k (1-a)^{n-k}}{p \times \binom{n}{k}\times a^k (1-a)^{n-k} + (1-p)\times \binom{n}{k}\times b^k (1-b)^{n-k}}.$$
Autres domaines où l’on rencontre des faux positifs
Bien entendu, il n’y a pas que dans le médical que l’on rencontre des faux positifs. Par exemple, si l’on analyse le comportement suspect des individus à l’aide d’une vidéo surveillance et d’un algorithme, ce dernier mettra en relief des individus au comportement jugé suspect alors que les individus ne présentent aucun danger.
En informatique, et plus précisément lors de l’utilisation d’anti-virus, un programme peut être détecté comme nuisible alors qu’il est totalement inoffensif.