Salut l’ami(e)! Sais-tu ce qu’est le surbooking (ou surréservation) ? Sais-tu que les compagnies aériennes vendent très souvent plus de billets que ne comporte de places l’avion du vol concerné ?
Nous allons étudier cela ensemble si tu veux bien… Sinon, ciao et bonne route à toi dans les méandres de la toile 😉
Surréservation (surbooking): un exemple pour commencer
Mise en place du problème
La compagnie Arnak’Air vend 105 billets d’avion pour un vol qui comporte 100 places.
La place est vendue 100 €. Si le client arrive à l’embarquement et qu’il n’y a plus de places, il est dédommagé à hauteur de 250 €.
En Europe, le règlement CE 261/2004 impose des indemnisations fixes pour les passagers victimes de surbooking, basées sur la distance du vol. Pour un vol de moins de 1500 km, elle s’élève à 250 €.
Pour simplifier les choses, nous n’allons pas considérer les clients qui se font rembourser leur billet avant le départ du vol… car nous sommes sur Arnak’Air et que ce n’est pas la politique de la maison! 🙂
On estime que la probabilité qu’un client ayant acheté un billet embarque réellement est égale à 0,95.
Formalisation du problème
Nous allons noter X la variable aléatoire représentant le nombre de passagers embarquant réellement sur ce vol. Alors, X suit la loi binomiale \(\mathcal{B}(105,0.95)\). On a alors la loi suivante:
| X | X ⩽ 100 | X = 101 | X = 102 | X = 103 | X = 104 | X = 105 |
| Probas. | 0.6076 | 0.1680 | 0.1252 | 0.0693 | 0.0253 | 0.0046 |
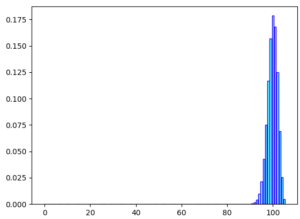
Exhaustion de cas sur le chiffre d’affaire (C.A.) de ce vol:
- Si au plus 100 passagers se présentent, le C.A. est égal à 100 × 100 = 10 000 €;
- Si 101 passagers se présentent, le C.A. est égal à 10 000 € – 1 × 250 € (dédommagement) = 9 750 €;
- Si 102 passagers se présentent, le C.A. est égal à 10 000 € – 2 × 250 € (dédommagement) = 9 500 €;
- Si 103 passagers se présentent, le C.A. est égal à 10 000 € – 3 × 250 € (dédommagement) = 9 250 €;
- Si 104 passagers se présentent, le C.A. est égal à 10 000 € – 4 × 250 € (dédommagement) = 9 000 €;
- Si 105 passagers se présentent, le C.A. est égal à 10 000 € – 5 × 250 € (dédommagement) = 8 750 €.
Si on note C la variable aléatoire correspondant au CA du vol, l’espérance mathématique de C est alors:
E(C) = 10 000×0.6076 + 9 750×0.1680 + 9 500×0.1252 + … + 8 750×0.0046 = 9812.375
Ainsi, la compagnie aérienne peut espérer avoir un chiffre d’affaire de 9812.375 €.
Surréservation (surbooking): optimisation du chiffre d’affaire
On cherche maintenant le nombre de billets pour optimiser le chiffre d’affaire, c’est-à-dire le rendre le plus grand possible. Pour cela, nous allons noter n le nombre de billets à vendre, n > 100.
Dans ce cas,
- Le CA généré par la vente des n billets est égal à 100n;
- Si n = 100 + k, alors le dédommagement s’élève à 250k.
À partir de cela, on peut exprimer l’espérance mathématique du chiffre d’affaire comme suit:$$E(C)=100n\times P(X\leqslant100) + \sum_{k=1}^{n-100} (100n-250k)\times P(X=k).$$
Nulle question d’e tenter d’exprimer algébriquement d’aller plus loin du point de vue algébrique ici. Cela serait ridicule. En effet, nous allons nous servir de Python pour déterminer la valeur de n pour laquelle E(C) est optimale.
from probastat import binom
def E(n):
X = binom(n,0.95)
s = 100*n + X.proba_cdf(100)
for k in range(1,n-99):
s += (100*n-250*k)*X.proba(100+k)
return s
n = 101
M = 10000
while True:
if E(n) > M:
M = E(n)
n += 1
print(n,M)
else:
print("Valeur maximale atteinte pour n =", n)
break
102 10156.395727676516
103 10538.21115720697
104 11361.376663985022
105 12708.638659358936
106 14433.538106350177
107 16236.015988536621
108 17825.23156864628
109 19036.042126823977
110 19845.99773814133
111 20325.129641238662
112 20573.85340106389
113 20681.87354363916
114 20712.818941198555
Valeur maximale atteinte pour n = 114Je précise ici que j’ai fait appel à mon propre module (car les autres sont, à mon goût, trop chiants à manipuler dès lors qu’il s’agit de calculer une probabilité).
La compagnie aérienne a dont intérêt à vendre 114 billets pour optimiser son chiffre d’affaire.

