Approximation d’une aire: méthode des trapèzes

Pour obtenir une approximation d’une aire sous une courbe, on peut utiliser la méthode des trapèzes.

En France, la méthode des rectangles est vaguement abordée au programme de mathématiques en classe de terminale. Mais ce n’est pas la méthode la plus intéressante, loin de là!

Approximation d’une aire sous une courbe par la méthode des trapèzes: introduction

Nous allons voir comment approximer l’aire du domaine délimité par la courbe représentative d’une fonction f continue sur un intervalle [a ; b] et l’axe des abscisses.

Pour cela, à l’instar de la méthode des rectangles, on commence par subdiviser l’intervalle [a ; b] en n subdivisions de même amplitude. Ensuite, on note:$$\forall~ 0\leq k \leq n,\quad x_k=a+k\frac{b-a}{n}.$$

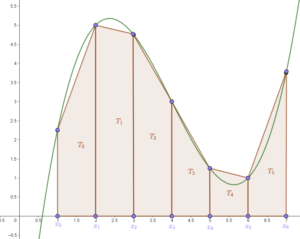
On considère alors les trapèzes \(T_k\) de bases \(f(x_k)\) et \(f(x_{k+1})\).

Un exemple avec n = 6

C’est un peu indigeste écrit comme cela, donc on va regarder ce que cela donne:

J’ai ici pris l’exemple de la fonction$$f(x)=\frac{1}{4}(x-4)^3-2(x-4)+3$$ et j’ai considéré l’intervalle [1 ; 7] que j’ai subdivisé en 6 intervalles d’amplitude 1.

Rappelons que l’aire d’un trapèze est donnée par la formule:$$\frac{(B+b)\times h}{2}$$où:

• B est la longueur de la grande base,
• b est celle de la petite base,
• h est la hauteur du trapèze.

Le trapèze \(T_k\) a donc pour aire:$$\mathcal{A}_k=\frac{1}{2}\Big[ \big( f(x_k)+f(x_{k+1}) \big) \times 1 \Big].$$

Approximation de l’aire sous la courbe

Il suffit maintenant d’ajouter l’aire de tous les trapèzes pour avoir une approximation (très grossière) de l’aire qui nous intéresse: $$\sum_{k=0}^6 \mathcal{A}_k = \frac{1}{2}\Big[ f(x_0) + 2f(x_1) + 2f(x_2) + \cdots + 2f(x_5) + f(x_6) \Big].$$

Calcul à l’aide de Python

Ici, trois lignes suffisent à calculer cette dernière somme:

f = lambda x: 0.25*(x-4)**3 - 2*(x-4) + 3
aire = 0.5 * sum( [ f(1) , f(7) ] + [ 2*f(x) for x in range(2,7) ] )
print( aire )

>>> 18.0

Calcul de l’aire avec intégrale

Notre aire se calcule à l’aide de l’intégrale:$$\int_1^7 f(x)\text{d}x.$$

Pour calculer cette intégrale on cherche une primitive de:$$f(x)=\frac{1}{4}x^3-3x^2+10x-5.$$ On trouve alors: $$F(x)=\frac{1}{16}x^4-x^3+5x^2-5x.$$

Maintenant, on a:$$\int_1^7 f(x)\text{d}x = F(7)-F(1)=17,0625 – (-0,9375) = 18.$$

On obtient exactement la même valeur que celle obtenue à l’aide de l’approximation précédente… Mais attention! Ceci est exceptionnel… En général, notre méthode des trapèzes ne donne réellement qu’une approximation.

Généralisation d’une formule de la méthode des trapèzes

Nous allons reprendre le raisonnement précédent en généralisant.

Dans un premier temps, nous subdivisons l’intervalle [a ; b] en n: la hauteur des trapèzes sera alors égale à \(\frac{b-a}{n}\).

Ensuite, l’aire du trapèze \(T_k\) sera égale à : \( \mathcal{A}_k = \frac{1}{2} \big(f(x_k)+f(x_{k+1})\big)\times\frac{b-a}{n}\).

On en conclut alors que la somme des aires des trapèzes est:$$\begin{array}{ll}\displaystyle\sum_{k=0}^n \mathcal{A}_k & = \displaystyle\frac{1}{2}\times\frac{b-a}{n}\sum_{k=0}^n \big(f(x_k)+f(x_{k+1})\big) \\ & = \frac{b-a}{2n}\Big[ f(x_0)+f(x_{n+1}) + 2\big( f(x_1)+f(x_2)+\cdots+f(x_n) \big)\Big]\end{array}$$

Premier code en Python

Si l’on souhaite un programme court, mais peu lisible, on peut opter pour le code suivant:

f = lambda x: 0.25*(x-4)**3 - 2*(x-4) + 3
n = 500
a, b = 1, 7
aire = ( (b-a) / (2*n) ) * sum( [ f(a) , f(b) ] + [ 2*f(a+k*(b-a)/n) for k in range(n) ] )
print( aire )

Mais je suis conscient qu’un tel programme n’est pas très digeste. Je vous propose alors le code suivant.

Second code en Python

def f(x):
    return 0.25*(x-4)**3 - 2*(x-4) + 3

def trapezoid_method(a,b,n):
    h = (b - a) / n # hauteur des trapèzes
    aire = 0
    for k in range(n):
        x1 = a + k*h
        x2 = a + (k+1)*h
        aire = aire + h*(f(x1) + f(x2))/2
        
    return aire

>>> trapezoid_method(1,7,500)
18.00000000000001

>>> trapezoid_method(1,7,50)
18.000000000000007

>>> trapezoid_method(1,7,10)
18.0

>>> trapezoid_method(1,7,5)
18.0