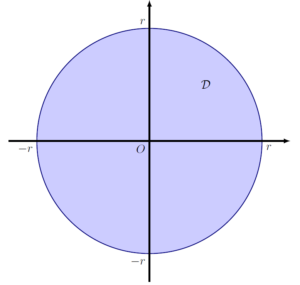
Considérons un disque de rayon r. Nous allons rapporté le plan à un repère orthonormé d’origine O, et nous allons centrer notre disque en O.
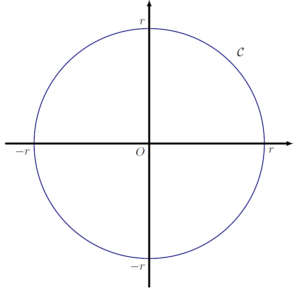
Afin de déterminer l’aire du disque, considérons uniquement son enveloppe : le cercle de centre O et de rayon r :
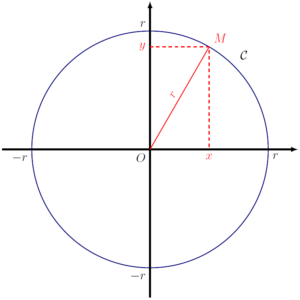
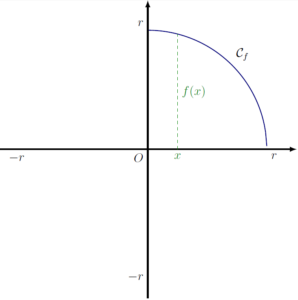
Maintenant, considérons un point M sur ce cercle d’abscisse x > 0 et d’ordonnée y > 0. Alors, d’après le théorème de Pythagore,$$x^2+y^2=r^2.$$
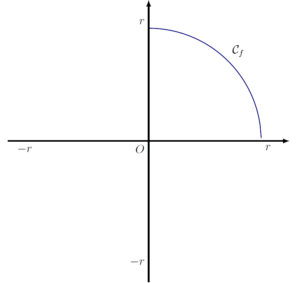
Ainsi,$$y=\sqrt{r^2-x^2}.$$On peut donc considérer le quart de cercle supérieur droit comme la représentation graphique de la fonction $f$ définie par:$$f(x)=\sqrt{r^2-x^2}$$sur [0;r].
Pour connaître l’aire du domaine délimité par l’axe des abscisses et la courbe représentative de f sur [0;r], il existe un outil mathématique : l’intégration. L’aire cherchée est:$$I=\int_0^rf(x)\text{d}x=\int_0^r\sqrt{r^2-x^2}\text{d}x.$$
Pour calculer une intégrale, il suffit de connaître une primitive de la fonction, mais en terminale, nous ne connaissons pas de primitive à la fonction f. On va donc utiliser une méthode pour arriver à nos fins (qui n’est pas au programme de Terminale, rassurez-vous).
Nous allons d’abord écrire f(x) autrement:$$\sqrt{r^2-x^2}=r\sqrt{1-\left(\frac{x}{r}\right)^2}.$$On peut ainsi écrire:$$I=r\int_0^r\sqrt{1-
\left(\frac{x}{r}\right)^2}\text{d}x.$$
Considérons alors une variable u telle que:$$u=\frac{x}{r}.$$Si x varie de 0 à r alors u varie de 0 à 1. De plus, si on considère u comme une fonction de x alors sa dérivée par rapport à x est:$$u'(x)=\frac{\text{d}u}{\text{d}x}=\frac{1}{r}.$$On peut alors écrire:$$\text{d}x=r\text {d}u.$$Ainsi, si nous voulons exprimer l’intégrale I en fonction de u, on écrit:$$I=r\int_0^1\sqrt{1-u^2}r\text{d}u=r^2\int_0^1\sqrt{1-u^2}\text{d}u .$$
Maintenant, la variable d’intégration est u, et varie de 0 à 1. On peut donc dire que c’est un sinus (par exemple). Posons alors:$$u=\sin(t).$$Alors,$$\text{d}u=\cos(t)\text{d}t.$$De plus, si u varie de 0 à 1 alors t varie de 0 à \(\frac{\pi}{2}\), d’où:$$I=r^2\int_0^{\frac{\pi}{2}}\sqrt{1-\sin^2(t)}\cos(t)\text{d}t=r^2\int_0^{\frac{\pi}{2}}\cos^2(t)\text{d}t.$$En effet, \(\cos^2(t)+\sin^2(t)=1\) donc \(1-\sin^2(t)=\cos^2(t)\); et comme t varie entre 0 et \(\frac{\pi}{2}\), son cosinus est positif donc \(\sqrt{\cos^2(t)})\cos(t)\) dans notre intégrale.
Il ne reste plus qu’à trouver une primitive de \(\cos^2(t)\). Pour cela, il faut se souvenir que:$$\cos(2t)=2\cos^2(t)-1$$et donc que:$$\cos^2(t)=\frac{1}{2}(\cos(2t)+1).$$Ainsi,$$\begin{align}I&=r^2\int_0^{\frac{\pi}{2}}\frac{1}{2}(\cos(2t)+1)\text{d}t\\&=\frac{r^2}{2}\int_0^{\frac{\pi}{2}}(\cos(2t)+1)\text{d}t\\&=\frac{r^2}{2}\left[ \frac{1}{2}\sin(2t)+t\right]_0^{\pi/2}\\&=\frac{r^2}{2}\times\frac{\pi}{2}\\&=\frac{\pi r^2}{4}. \end{align}$$
L’aire du disque étant égale au quadruple de l’aire trouvée, on obtient finalement que l’aire du disque est égale à :$$\mathcal{A}_{\mathcal{D}}=4I=\pi r^2.$$
Une précision sur l’outil d’intégration
Pour un réel x quelconque de l’intervalle [0;r], le segment tracé a une longueur égale à f(x).
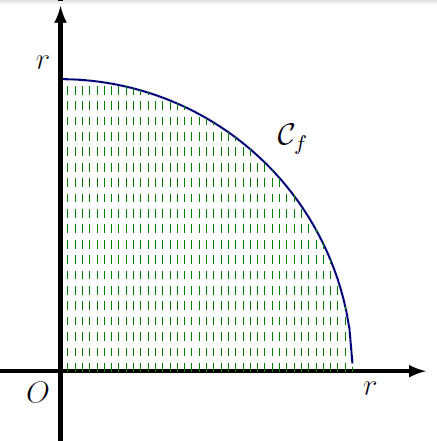
Trouver l’aire du quart de cercle revient à « additionner » la longueur de tous les segments obtenus en faisant varier x de 0 à r. Mais x est un nombre réel donc il existe une infinité de valeurs. On ne peut donc pas additionner « une à une » toutes ces longueurs. On dit que la somme n’est pas discrète (une somme discrète est une somme où l’on peut compter un à un tous ses termes, même s’il y en a une infinité, comme 1+2+3+…). La somme est qualifiée de continue. Et donc l’intégrale représente une somme continue.
Sur le schéma ci-dessus, il faut imaginer que l’on rapproche de plus en plus les segments jusqu’à ce qu’ils soient tous « collés ». Ils couvrent alors toute la surface. Ainsi, la somme de leurs longueurs sera égale à l’aire.
Avec cela, nous pouvons continuer et nous demander pourquoi le volume d’une boule est égal à \(\frac{4}{3}\pi r^3\) : c’est l’objet de l’article suivant.



Bonjour et merci pour cette claire démonstration
Juste un point « u varie de 0 à 1.on peut donc dire que c’est un sinus( par exemple) » pouvez vous développer cela , c’est à dire justifier l’emploi de ce sinus (ou autre) c’est à dire quelle doit être le profil de la fonction qu’on substitue a u pour intégrer? Merci d’avance.
Bonjour. Il n’y a pas de « profil » à proprement parlé.Si une variable d’intégration varie entre 0 et 1, on peut toujours la voir comme un sinus ou un cosinus (si cela arrange et facilite le calcul, ce qui est le cas ici). Si vous avez \(\int_0^1 x^2 \text{d}x\), vous pouvez faire de même, mais cela ne facilite pas le calcul.
« Pour calculer une intégrale, il faut connaître une primitive de la fonction »
Non, il ne « faut » pas, il « suffit » de connaître une primitive mais il existe d’autres méthodes (par exemple si la fonction est impaire et le domaine d’intégration est symétrique par rapport à 0, ou des techniques plus élaborées qui passent par les nombres complexes, les séries entières ou l’introduction d’une fonction à plusieurs variables).
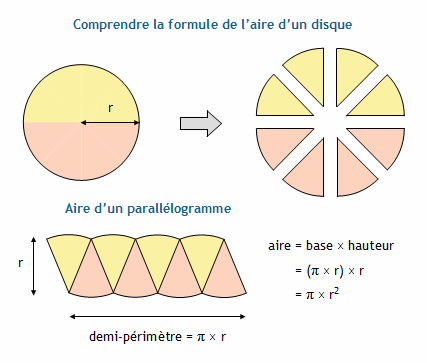
En collège, on ’a pas le calcul intégral mais on peut illustrer le pourquoi du comment avec des quartiers d’orange. L’idée viendrait d’Archimède :
Oui, il y a abus de langage ici de ma part. Il faut rectifier cela en effet.
Bonjour.
Quelque chose me tracasse dans votre démonstration car, selon la définition que que sous-entendez pour la fonction sinus, il est possible que l’on tourne en rond. Permettez-moi de vous exposer ce qui me turlupine…
Si vous définissez la fonction sinus à partir de sa série entière (basée sur l’exponentielle complexe), alors là, aucun problème car il est évident que sa dérivée est la fonction cosinus.
En revanche, si vous définissez la fonction sinus, comme on le fait en analyse réelle, par l’ordonnée du point correspondant sur le cercle trigonométrique alors, dans ce cas, il faut, pour prouver que sa fonction dérivée est la fonction cosinus, connaître la limite en 0 de sin(x)/x. Or, et c’est là que je pense qu’il peut y avoir un problème, il est nécessaire de connaître au préalable l’aire d’un disque pour déterminer cette limite.
Voilà ce qui m’embête. À moins que je n’ai raté quelque chose.
Cordialement.
Très intéressante approche et chapeau pour les substitutions.
J’aurais une autre approche. Bien qu’elle donne le bon résultat, je n’arrive pas à savoir si elle est valide (et je ne sais pas si elle a déjà été présentée)
Elle consiste à voir la surface du disque comme la composition de petites surfaces circulaires concentrique.
En se plaçant dans un référentiel polaire [r, \(\theta\)], chacune de ces surfaces aurait une surface égale à \( P(r) \times \text{d}r = 2\pi r \text{d}r\).
En cherchant la surface S d’un disque de rayon R : $$S = \int_0^R 2\pi r \text{d}r = 2\pi \int_0^R r \text{d}r= \pi R^2.$$(CQFD)
Je trouve la démo plus simple, moins de notion d’intégration à connaitre et plutôt intuitive sur le prédicat (si il est valide).
Cordialement,
J’ai du mal à comprendre cette logique. Déjà, « voir la surface du disque comme la composition de petites surfaces circulaires concentriques » me paraît faux. Quand on calcule une intégrale, on ajoute. Or, en prenant des disques concentriques, ils se chevauchent donc là, je ne vois pas comment la somme des aires de ces disques pourraient correspondre à celle du disque initial. De plus, en voulant utiliser des coordonnées polaires, il faudrait peut-être faire intervenir \(r\), mais aussi \(\theta\); or, je ne le vois nulle part dans les calculs.
À mon avis, cette façon de voir n’est pas plus simple que d’autres, et est même fausse. À moins que je l’aie mal comprise.
ce n’est pas une somme des aires mais des circonférences… qui donnent l’air, donc la démo est toute à fait juste…
Je viens de relire ce qui a été écrit précédemment et je viens enfin de comprendre. La raison pour laquelle je suis passé à côté de la réelle signification est le vocabulaire faux: on ne dit pas « composition de cercles » (mathématiquement, c’est faux) et c’est ce que je ne comprenait pas.
Pour expliquer correctement, on peut en effet voir l’aire du disque de rayon R comme étant LA SOMME des périmètres des cercles concentriques de centre O et de rayon \(r\) variant de 0 à R, ce qui donne bien \(\displaystyle\int_0^R 2\pi r\text{d}r=\pi R^2.\)
La démonstration est donc en effet correcte vue comme ceci (inutile de passer en coordonnées polaires d’ailleurs). D’où l’importance de choisir le bon vocabulaire pour se faire comprendre des plus « naïf » ( comme moi 🙂 ).
Bonjour,
Je comprends que u'(x)=du/dx et que dx=(1/u'(x))du
Mais pouvez vous m’expliquer pourquoi du=cos(t)dt et non du=(1/cos(t))dt
Si u(x) = sin(t)dt alors la dérivée de la fonction u est bien cos(t) non ? Donc du = sin(t)dt. C’est une notation pour dire que la dérivée de la fonction u par rapport à la variable t est sin(t).
bonjour
la démonstration par l’intégrale en coordonnées polaires est beaucoup plus accessible
Cdlt
En effet, mais je souhaitais montrer un autre type de calculs 🙂