Une vidéo de la chaîne Numberphile me fascine :
Le nombre suivant:
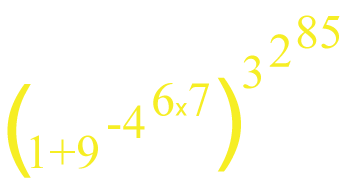
est presque égal à e.
Pour s’en convaincre, il faut avoir en tête que: $$\displaystyle\lim\limits_{n\to+\infty}\left(1+\frac{1}{n}\right)^n=\text{e}.$$
Et puis, il faut aussi voir que:$$3^{2^{85}}=3^{2\times2^{84}}=9^{2^{84}}.$$De plus, $$2^{84}=4^{42}=4^{6\times7}.$$Ainsi, $$3^{2^{85}}=9^{4^{6\times7}}.$$
En posant \(N= 9^{4^{6\times7}}\), on a \(\frac{1}{N}= 9^{-4^{6\times7}} \) et le nombre écrit ci-dessus s’écrit : \( E=\left(1+\frac{1}{N}\right)^N \).
Or, \(N\) est très grand, et ceci justifie que \(E \approx \text{e}\).
Pour aller plus loin
J’ai envie de calculer le nombre de chiffres de \(N\) pour justifier qu’il est vraiment très grand. Pour cela, j’utilise la formule : $$p=\text{E}\big(\log N\big)+1$$où \(p\) représente le nombre de chiffres de \(N\).
\(\log N=4^{42}\log 9\). Comme \(9\approx10\), on peut assimiler \(\log 9\) à 1. Ainsi, \(\log N\approx4^{42}\), nombre à 26 chiffres, donc de l’ordre du Yota (\(10^{24}\)). Par conséquent, le nombre de chiffres de \(N\) est de l’ordre du Yote, ce qui justifie bien que \(N\) est réellement très grand, et donc que \(E\) soit très proche de \(\text{e}\).
rLe fait remarquable est que \(E\) est écrit avec tous les chiffres de 1 à 9 mis une seule fois, et il donne une valeur approchée de e et ses 18 Yota premiers chiffres sont corrects ! Nombre de chiffres corrects dans l’approximation :
18 457 734 525 360 901 453 873 570.
Le nombre que j’ai noté \(E\)a été découvert par Richard Sabey (dont je ne sais pas grand chose…).


