Introduction aux matrices de rotation

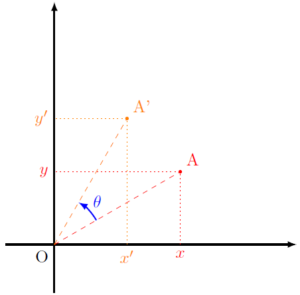
Considérons la configuration suivante :

Dans le repère orthonormé d’origine O, A(x;y) est un point quelconque et A'(x’;y’) est son image par la rotation de centre O et d’angle \(\theta\). On cherche à exprimer x’ et y’ en fonction de x, y et \(\theta\)…

Un peu de trigonométrie

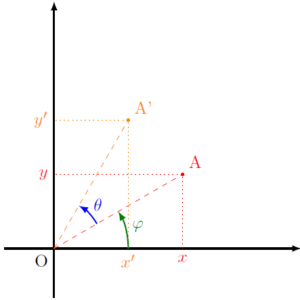
Complétons la figure précédente en introduisant un angle :

Dans le triangle rectangle rouge (OAx), on a : $$(1)\qquad\begin{cases}x&=OA\cos\varphi\\y&=OA\sin\varphi\end{cases}$$

Dans le triangle rectangle orange (OA’x’), on a : $$\begin{cases}x’&=OA’\cos(\theta+\varphi)=OA’\big[\cos\theta\cos\varphi-\sin\theta\sin\varphi \big]\\y’&=OA’\sin(\theta+\varphi)=OA’\big[\sin\theta\cos\varphi+\sin\varphi\cos\theta \big]\end{cases}$$Or, OA = OA’ donc ceci revient à écrire, en tenant compte des égalités (1) : $$\begin{cases}x’ & = x\cos\theta\ – y\sin\theta\\y’ & = x\sin\theta + y\cos\theta\end{cases}$$

Notation matricielle

Du système : $$\begin{cases}x’ & = x\boxed{\cos\theta}+ y\boxed{-\sin\theta}\\y’ & = x\boxed{\sin\theta} + y\boxed{\cos\theta}\end{cases}$$ on peut “extraire” les coefficients encadrés et les mettre dans un tableau: $$\begin{array}{|c|c|}\hline\cos\theta & -\sin\theta\\\hline\sin\theta & \cos\theta\\\hline\end{array}$$que l’on va tout de suite représenter différemment, pour simplifier, sous la forme suivante : $$\begin{pmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{pmatrix}.$$C’est cette représentation que l’on va appeler “matrice de rotation”. Le système : $$\begin{cases}x’ & = x\cos\theta\ – y\sin\theta\\y’ & = x\sin\theta + y\cos\theta\end{cases}$$ peut alors s’écrire de manière matricielle ainsi : $$\begin{pmatrix}x’\\y’\end{pmatrix}= \begin{pmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{pmatrix} \begin{pmatrix}x \\ y\end{pmatrix}.$$

Obtenir une équation de la droite image par rotation

Considérons une droite (d) d’équation réduite \( y = mx + p\). Cherchons une équation cartésienne de l’image (d’) de (d) par la rotation de centre O et d’angle \(\theta\).

Notons \(\vec{u}\binom{1}{m}\) un vecteur directeur de (d) et \(\vec{u’}\binom{a}{b}\) un vecteur directeur de (d’) de sorte que \(\|\vec{u}\|^2=\|\vec{u’}\|^2=1+m^2\). Alors,$$\vec{u}\cdot\vec{u’}=\|\vec{u}\|\times\|\vec{u’}\|\times\cos\theta=(1+m^2)\cos\theta$$et par suite:$$\begin{cases}a^2+b^2&=1+m^2\\\vec{u}\cdot\vec{u’}&=a+bm=(1+m^2)\cos\theta\end{cases}$$

On peut alors écrire, dans un premier temps:$$a=(1+m^2)\cos\theta-bm$$ et en substituant dans l ‘autre équation, on obtient ensuite:$$(1+m^2)^2\cos^2\theta-2bm(1+m^2)\cos\theta+(1+m^2)b^2=1+m^2$$soit, en simplifiant par \(1+m^2\):$$b^2-(2m\cos\theta) b+(1+m^2)\cos^2\theta-1=0.$$C’est une équation du second degré en \(b\) des discriminant:$$\Delta=4m^2\cos^2\theta-4\big[ (1+m^2)\cos^2\theta-1\big] = 4\sin^2\theta.$$dont une solution est, par exemple:$$b=m\cos\theta+|\sin\theta|.$$On en déduit alors:$$a=\cos\theta-m|\sin\theta|.$$

Une équation cartésienne de (d’) est donc de la forme:$$bx-ay+c=0.$$Or, le point de coordonnées \( \begin{pmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{pmatrix} \begin{pmatrix}0 \\ p\end{pmatrix} = \begin{pmatrix}-p\sin\theta \\ p\cos\theta\end{pmatrix} \) appartient à (d’), comme image du point d’intersection de (d) avec l’axe des ordonnées par la rotation r. On en déduit alors que:$$c=pa\cos\theta+pb\sin\theta.$$Une équation cartésienne de (d’) est donc:$$\begin{array}{l}\big(m\cos\theta+|\sin\theta|\big)x+\big(m|\sin\theta|-\cos\theta\big)y\\+p\sin\theta\big(m\cos\theta+|\sin\theta|\big)+p\cos\theta\big(\cos\theta-m|\sin\theta|\big)=0\end{array}$$

Un peu de Python

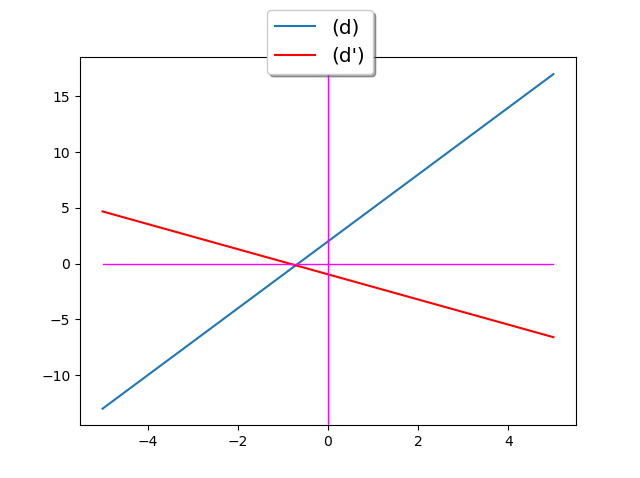
Si nous avons fait cela, c’est peut-être pour nous simplifier la vie un peu plus tard… On peut, avec cette dernière formule, écrire un programme Python qui nous donne directement une équation cartésienne de (d’) en fonction des paramètres m et p que l’on entre au clavier.

from math import cos,sin,pi
import matplotlib.pyplot as plt

m = float(input("Entrer le coefficient directeur 'm' : "))
p = float(input("Entrer l'ordonnée à l'origine 'p' : "))
t = float(input("Entrer l'angle de la rotation de centre O (en degré) : "))
t = t*pi/180

a = m*cos(t) + abs( sin(t) )
b = m*abs( sin(t) ) - cos(t)
c = p*sin(t)*a - p*cos(t)*b

if b<0:
    bs = " - "+str(abs(b))
else:
    bs = " + "+str(b)

if c<0:
    cs = " - "+str(abs(c))
else:
    cs = " + "+str(c)

print(str(a)+"x"+bs+"y"+cs+" = 0")

# tracé

fig = plt.figure()


axes = fig.add_subplot(111)
axes.set_frame_on(True)

axes.yaxis.tick_left()
axes.xaxis.set_visible(True)
(xmin, xmax) = (-5,5)
(ymin, ymax) = (-20,20)
axes.add_artist(plt.Line2D((xmin, xmax), (0, 0),
                              color = 'magenta', linewidth = 1))
axes.add_artist(plt.Line2D((0, 0), (ymin, ymax),
                              color = 'magenta', linewidth = 1))



x = [-5 , 5]
y = [-5*m+p , 5*m+p]

plt.plot(x,y,label='(d)')

y = [-a*(-5)/b-c/b , -a*5/b-c/b]

plt.plot(x,y,color='r',label="(d')")

legend = fig.legend(loc='upper center', shadow=True, fontsize='x-large')

plt.show()

Par défaut, le repère n’étant pas orthonormé, l’angle que l’on voit n’est pas représentatif. Voyons donc un autre code :

from math import cos,sin,pi
import matplotlib.pyplot as plt

m = float(input("Entrer le coefficient directeur 'm' : "))
p = float(input("Entrer l'ordonnée à l'origine 'p' : "))
t = float(input("Entrer l'angle de la rotation de centre O (en degré) : "))
t = t*pi/180

a = m*cos(t) + abs( sin(t) )
b = m*abs( sin(t) ) - cos(t)
c = p*sin(t)*a - p*cos(t)*b

if b<0:
    bs = " - "+str(abs(b))
else:
    bs = " + "+str(b)

if c<0:
    cs = " - "+str(abs(c))
else:
    cs = " + "+str(c)

print(str(a)+"x"+bs+"y"+cs+" = 0")

# tracé

fig = plt.figure()

plt.axis('equal')
plt.grid(axis='both',color='lightgray', linestyle='--')


x = [-8 , 8]
y = [0 , 0]
plt.plot(x,y,linewidth=1,color='black')

x = [0 , 0]
y = [-6 , 6]
plt.plot(x,y,linewidth=1,color='black')


x = [-5 , 5]
y = [-5*m+p , 5*m+p]

plt.plot(x,y,label='(d)')

y = [-a*(-5)/b-c/b , -a*5/b-c/b]

plt.plot(x,y,color='r',label="(d')")

legend = fig.legend(loc='upper center', shadow=True, fontsize='x-large')

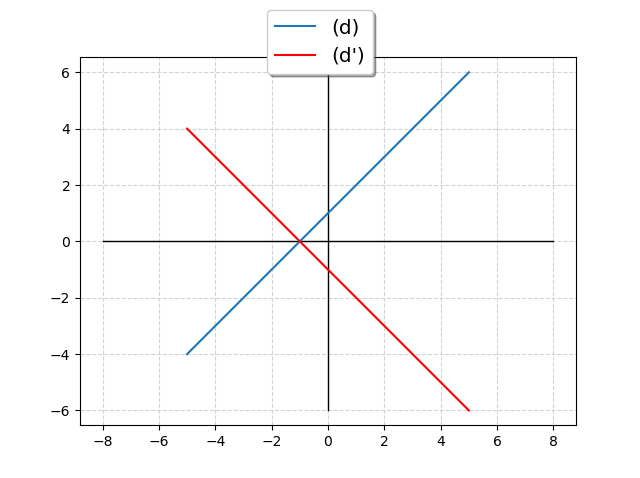
plt.show()

Sur ce dernier exemple, on voit parfaitement l’angle de la rotation (ici, 90°).