Etude d’une suite définie par \(u_{n+1} = f(u_n)\)

C’est un classique dans l’étude des suites : on considère une fonction f et on définit une suite par son premier terme \(u_0\) et par la relation \(u_{n+1}=f(u_n)\) pour tout entier naturel n.

Voyons cela avec l’exemple où \(f(x)=\frac{ax+b}{x^2-3x+2}\)…

Recherche de a et b

Je construis ma fonction en ayant à l’esprit que le dénominateur s’annule pour x = 1 et x = 2. J’aimerais que ma suite tombe sur \(u_k = 1\), donc je veux que l’équation f(x) = 1 ait une solution, et tant qu’à faire, autant que cette solution soit sans radical donc qu’elle ait un discriminant sympathique.$$ f(x)=1 \iff x^2 – (3+a)x + 2-b = 0$$et le discriminant de cette équation est :$$\Delta=1+6a+a^2+4b.$$J’aimerais donc que ce dernier soit un carré parfait pour simplifier mes calculs. Je vais donc faire appel à Python:

from math import sqrt

c = [(a,b) for a in range(1,20) for b in range(1,20) if 1+6*a+a*a+4*b >= 0 and int(sqrt(1+6*a+a*a+4*b)) == sqrt(1+6*a+a*a+4*b) ]

for i in c:
    print(i,1+6*i[0]+i[0]*i[0]+4*i[1])

J’obtiens les couples suivants:

 (1, 2) 16
 (1, 7) 36
 (1, 14) 64
 (2, 2) 25
 (2, 8) 49
 (2, 16) 81
 (3, 2) 36
 (3, 9) 64
 (3, 18) 100
 (4, 2) 49
 (4, 10) 81
 (5, 2) 64
 (5, 11) 100
 (6, 2) 81
 (6, 12) 121
 (7, 2) 100
 (7, 13) 144
 (8, 2) 121
 (8, 14) 169
 (9, 2) 144
 (9, 15) 196
 (10, 2) 169
 (10, 16) 225
 (11, 2) 196
 (11, 17) 256
 (12, 2) 225
 (12, 18) 289
 (13, 2) 256
 (13, 19) 324
 (14, 2) 289
 (15, 2) 324
 (16, 2) 361
 (17, 2) 400
 (18, 2) 441
 (19, 2) 484

Un seul me suffit, donc j’en prends un au hasard : disons (3,2) pour que la fraction ne se simplifie pas. Ma fonction sera donc :$$f(x)=\frac{3x+2}{x^2-3x+2}.$$Dans ce cas, $$\Delta=36$$et les solutions sont x = 0 et x = 6.

Ainsi, en prenant \(u_0=6\), je suis assuré que la suite s’arrêtera très vite. Je peux donc proposer comme début d’énoncé :

On considère la suite \(u_n\) de premier terme \(u_0=a\) telle que, pour tout entier naturel n, \(u_{n+1}=\frac{3x+2}{x^2-3x+2}\). Montrer que si a = 6 alors cette suite n’est pas définie.

Moins de calculs…

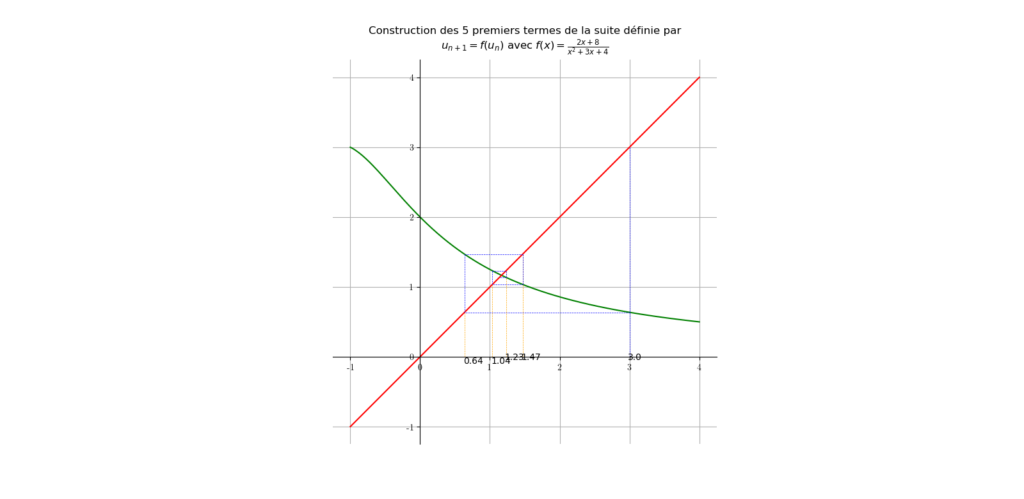
Conscient de la longueur du raisonnement pour une si petit question, et surtout pour s’assurer que notre suite est bien définie, on peut utiliser le programme Python suivant:

x = 3

for i in range(100):
    try:
        x = (2*x + 8) / (x*x + 3*x + 4)
        print(x)
    except:
        print("C'est fini !")
        break

J’ai ici changé ma suite car la première n’avait que peu d’intérêt à mes yeux. Celle-ci converge… et le programme nous le fait conjecturer à la vue de ce qu’il affiche:

 0.6363636363636364
 1.468586387434555
 1.0354714748303893
 1.231375020248727
 1.135970125876628
 1.1809083132856442
 1.1593940141088968
 1.1696154661004132
 1.1647414040944077
 1.1670615364996197
 1.165956197820842
 1.166482586073047
 1.166231860376169
 1.1663512736301962
 1.1662943981884963
 1.1663214868901877
 1.1663085849266617
 1.1663147299200987
 1.166311803154159
 1.1663131971263379
 1.166312533199176
 1.1663128494172315
 1.1663126988075323
 1.1663127705405656
 1.1663127363752483
 1.1663127526476522
 1.1663127448973616

Pour être honnête avec vous, la suite n’est qu’un prétexte pour montrer un exemple de la commande try de Python. Car après tout, l’étude de la convergence est assez simple ! On a en effet une configuration dite en escargot :

Toutefois, la fonction étant décroissante, l’étude est légèrement plus longue que dans le cas où la fonction est croissante, mais ça… c’est une autre histoire!