Enveloppe astroïdale Python avec Turtle

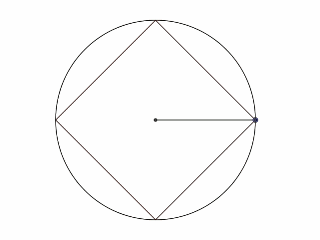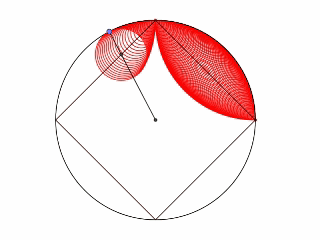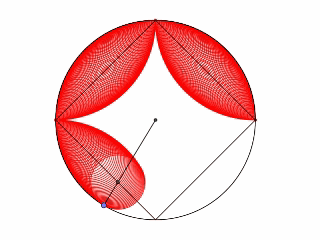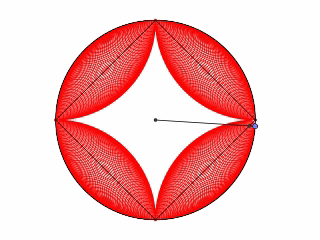
L’objectif de cet article est de construire une enveloppe astroïdale en Python avec cette suite de cercles rouges; on va utiliser pour cela le module Turtle.

Enveloppe astroïdale en Python : approche mathématique

Avant toute chose, il est nécessaire de comprendre comment sont obtenus tous les cercles rouges.

Si on regarde et analyse bien la figure, les tracés suggèrent que pour un angle \(\alpha\) donné, exprimé en degré, on trace un segment d’origine O (si on se place dans un repère, c’est l’origine) et d’angle \(\alpha\), qui coupe l’un des côté du carré inscrit dans le cercle principal.

Prenons le côté en haut à droite (donc dans le quadrant x > 0 et y > 0 si on se ramène à un repère). Il a pour équation \(y=-x+R\) si on considère que le cercle principal a pour rayon \(R\). Notons I le point d’intersection de la droite d’équation \(y = x\tan(\alpha)\), qui forme un angle de \(\alpha\) avec l’horizontale, avec le segment d’équation \(y=-x+R\). Alors, ses coordonnées vérifient:$$\begin{cases}y_I=-x_I+R\\y_I=x_I\tan(\alpha)\end{cases} $$Donc:$$x_I\tan(\alpha)=-x_I+R$$d’où:$$x_I=\frac{R}{\tan(\alpha)+R}.$$

Une fois les coordonnées de I connues, on calcule la longueur IM, où M est le point du cercle principal de coordonnées \(R\cos\alpha;R\sin\alpha)\), à l’aide de la formule vue en classe de Seconde:$$IM = \sqrt{(x_I-x_M)^2 + (y_I-y_M)^2}.$$On peut alors tracer le cercle de centre I et de rayon IM : c’est un des cercles rouges.

Avec Turtle

Il faut faire appel à quelques méthodes du module Turtle; inutile donc d’écrire:

from turtle import *

En effet, le mieux est de n’importer que les méthodes qui nous intéressent. Il en est de même pour le module math, où seules les méthodes sin, cos, tan et pi sont nécessaires (pour la racine carrée, on élève à la puissance 0.5).

On commence donc par tracer un cercle (avec Turtle, c’est un peu… comment dire poliment ? … je trouve pas ! Désolé !) en se déplaçant d’abord en bas de la fenêtre puis en traçant le cercle. Ensuite, on en profite pour tracer le carré inscrit dans le cercle (avec “goto”, comme le stylo est déjà baissé, ça trace les segments).

Maintenant, on fait une boucle itérative sur l’angle variant de 0 à 359. Si vous observez bien, je ne me suis pas embêté avec les cas où l’angle est égal à 90°, 180° et 270° car ça n’a que peu d’importance au final du point de vue visuel). En fait 180° ne pose pas de problème pour la tangente, mais peu importe… Ouais, je suis une grosse feignasse !…

Remarquez aussi que j’ai pris \(R=300\) car la fenêtre par défaut fait 800×800. “300” me semblait un bon compromis. Voilà donc le programme:

Alors là, les plus observateurs.trices. d’entre vous me diront : “t’es qu’un charlatant ! Le GIF n’est pas exactement ce que fait ce programme…” et c’est vrai ! C’est en fait un ancien GIF qui traînait sur mon disque dur… quand je vous disais que j’étais une grosse feignasse ! En fait, l’image finale donne ceci:

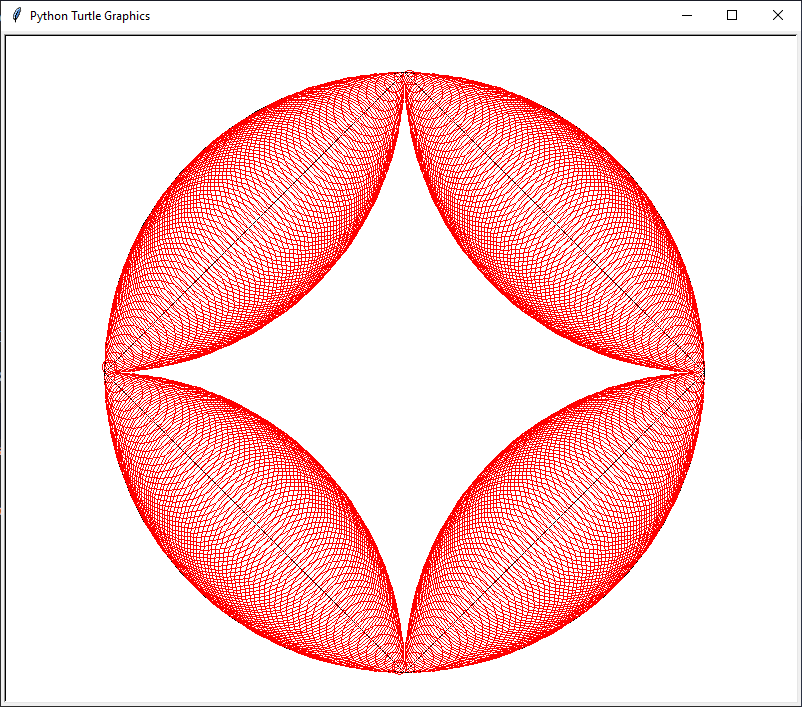
En attendant, si vous souhaitez télécharger le programme directement plutôt que de vous embêter à le réécrire à la main, c’est ci-dessous pour les abonné·e·s: