Dans les programmes de 1ère Spécialité Math, il est question de trigonométrie… Et c’est la période de l’année où les professeur.e.s peuvent aborder cette notion avec leurs élèves. J’ai donc voulu écrire un programme Python permettant de trouver la mesure principale d’un angle s’écrivant sous la forme \(\displaystyle\frac{a\pi}{b}\), c’est-à-dire la mesure comprise dans l’intervalle \(]-\pi;\pi]\) équivalente à celle donnée modulo \(2\pi\).
Rappels mathématiques
Sur un exemple
On considère l’angle de mesure \(\displaystyle\frac{101\pi}{7}\).
- Étape 1 : effectuer la division euclidienne de 101 par 7. Petit flash-back de 6ème… on écrit : \(101 = 7 \times 14 + 3\). Certains calculatrices permettent d’obtenir le quotient (14) et le reste (3), mais sinon, il suffit de prendre la partie entière de \(101 \div 7\), soit de 14,428… et ensuite de faire \(101-14\times7\) pour obtenir le reste.
- Étape 2 : on revient à la mesure de l’angle. $$\frac{101\pi}{7}=\frac{(7\times14+3)\pi}{7}=14\pi + \frac{3\pi}{7}.$$On remplace le coefficient de \(\pi\) par son écriture en division euclidienne, puis on coupe la fraction en deux, l’intérêt étant que la première fraction obtenue est simplifiable et donne le quotient précédemment obtenu (ici, 14).
- Étape 3 : on simplifie. Modulo \(2\pi\), \(14\pi=0\) car 14 est un nombre pair (donc, sur le cercle trigonométrique, il se place au même endroit que 0). Ainsi, l’angle trouvé est égal, modulo \(2\pi\), à \(\displaystyle\frac{3\pi}{7}\). On vient d’obtenir la mesure principale de l’angle initial.
Si le quotient de la division euclidienne avait été impair, par exemple \(21\pi\), on l’aurait remplacé par \(-\pi\), puis on l’aurait ajouté au reste. Par exemple,$$21\pi+\frac{2\pi}{7}=-\pi+\frac{2\pi}{7}=-\frac{5\pi}{7}$$Avec cette méthode, on obtient toujours la mesure principale de l’angle.
Cas général
On a un angle de mesure \(\displaystyle\frac{a\pi}{b}\).
- Étape 1 : \(a = bq + r,\ 0 \leq r < b\)
- Étape 2 : \(\displaystyle\frac{a\pi}{b}=q\pi+\frac{r\pi}{b}\)
- Étape 3 : si \(q\) est pair, alors la mesure principale est \(\displaystyle\frac{r\pi}{b}\), sinon c’est \(-\pi + \displaystyle\frac{r\pi}{b} = \frac{(r-b)\pi}{b}\).
En Python
Nous avons maintenant tous les outils pour écrire un programme en Python. Bien sûr, il n’existe pas qu’une seule façon d’écrire le programme. Selon la logique employée, il pourra être plus ou moins long.
Pour ma part, j’ai choisi d’insérer une fonction pour placer le point, à l’aide du module turtle.
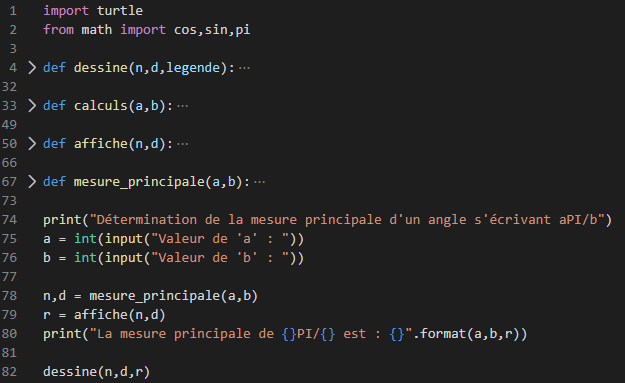
J’ai choisi de créer trois fonctions : l’une calcule la mesure principale, l’autre permet de l’afficher (en fonction des coefficients trouvés, l’affichage doit changer – cas où le numérateur trouvé est un multiple du dénominateur –> simplification, etc.) et une dernière pour tracer le cercle trigonométrique et le point.
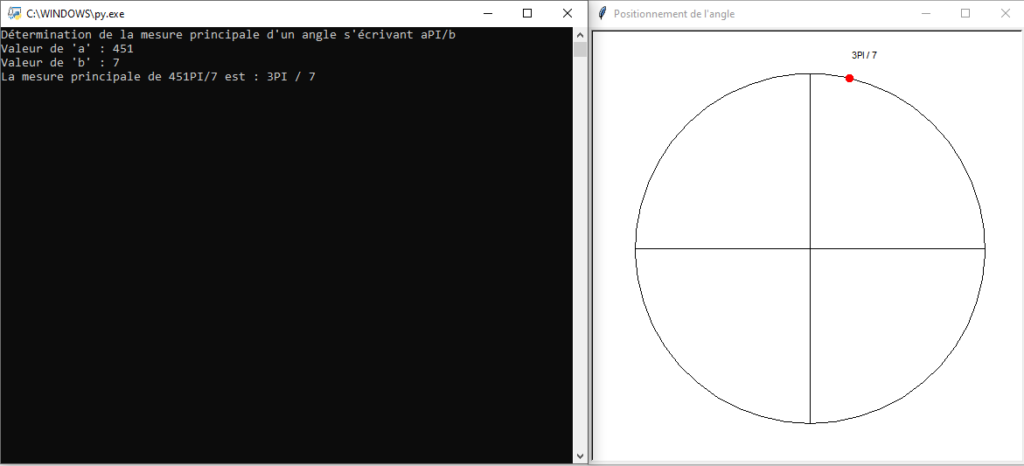
Le script Python se trouve dans un fichier ZIP ci-dessous:



Bonjour, Ou se trouve le fichier Zip de la mesure principale d’un angle avec Python? Merci de votre réponse;
Vérifiez vos emails s’il vous plaît. Une réponse a été envoyée dès votre premier message.