Le problème est le suivant : trouver l’aire du domaine représenté en bleu sur la figure ci-dessous:
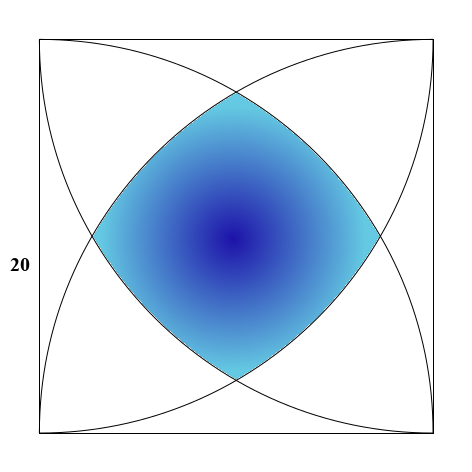
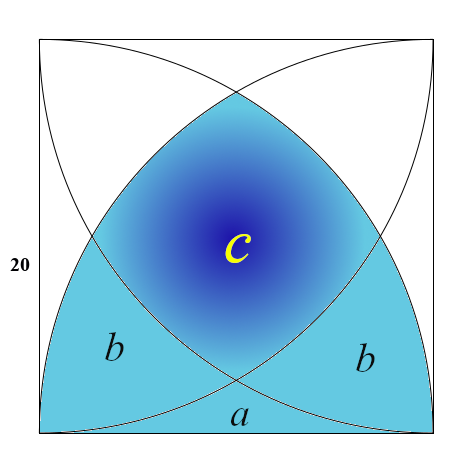
Dans un premier temps, notons a, b et c l’aire des différentes parties comme indiqué ci-dessous:
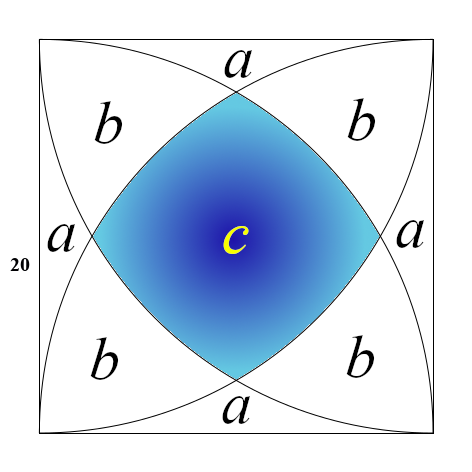
L’aire totale valant 20², soit 400, on peut déjà établir une égalité: $$4a+4b+c=400.$$
Maintenant, si nous ne considérons que le quart de cercle inférieur gauche (par exemple) :
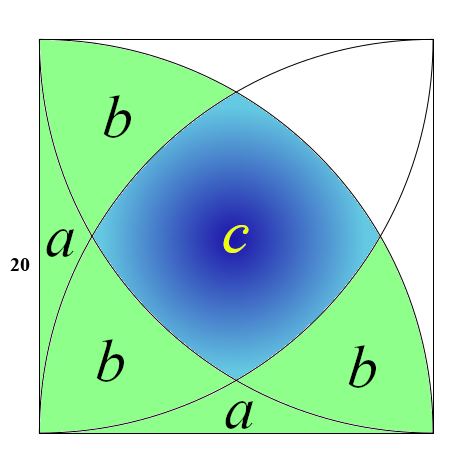
nous pouvons établir l’égalité:$$2a+3b+c=100\pi.$$
Maintenant, considérons le secteur angulaire représenté en orange sur la figure ci-dessous:
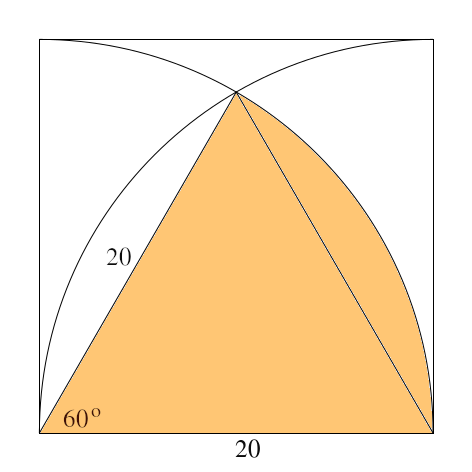
Ce secteur angulaire a pour aire:$$20^2\pi\times\frac{60}{360}=\frac{200\pi}{3}.$$De plus, l’aire du triangle équilatéral est:$$20^2\frac{\sqrt3}{4}=100\sqrt3.$$On en déduit alors que l’aire de la partie colorée sur la figure ci-dessous est:
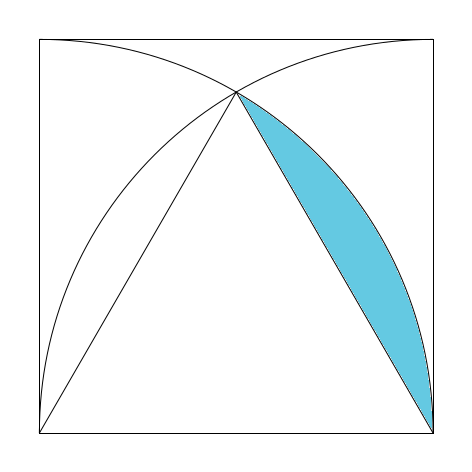
$$\frac{200\pi}{3}-100\sqrt3.$$ On déduit que l’aire du domaine coloré sur la figure ci-dessous est:
$$a+2b+c=\left(\frac{200\pi}{3}\right)+\left(\frac{200\pi}{3}-100\sqrt3\right).$$ Nous avons désormais un système de trois équations à trois inconnues:$$\begin{cases}4a+4b+c=400\\2a+3b+c=100\pi\\a+2b+c=\frac{400\pi-300\sqrt3}{3} \end{cases}$$À l’aide de XCAS (par exemple), je trouve la valeur de c:
La valeur de c est donc:$$c=400\left(\frac{\pi}{3}-\sqrt3+1\right).$$
Cet article est tiré de la vidéo:



