La question est simple : quelle est la longueur AE dans la figure suivante ?
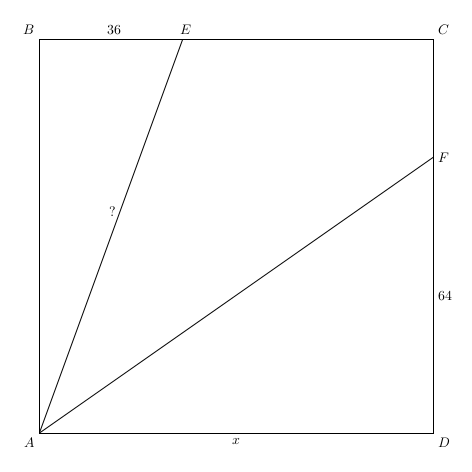
Nous savons que ABCD est un carré et que (AF) est la bissectrice de \(\widehat{DAE}\). Nous avons noté \(x = AD\) la longueur d’un côté de ce carré, mais nous n’en avons pas nécessairement besoin.
1ère approche : abordable au collège
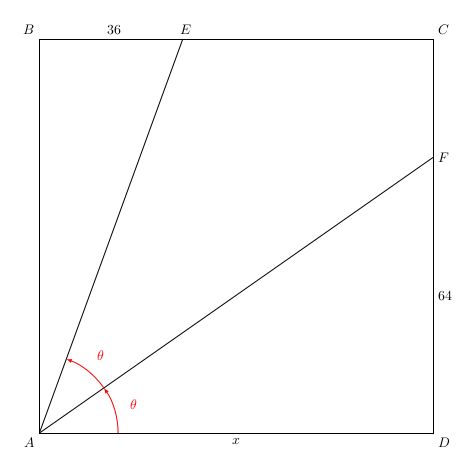
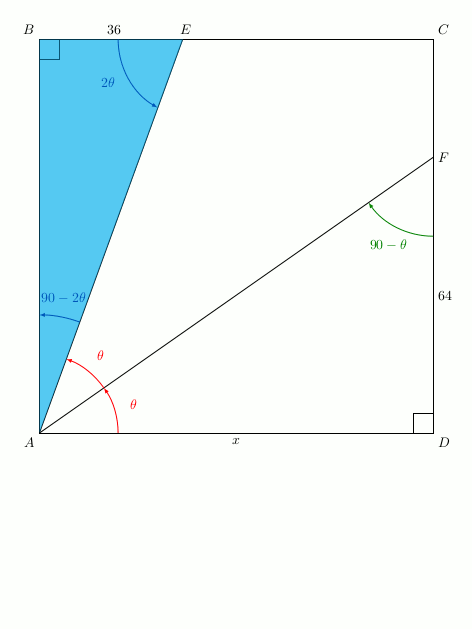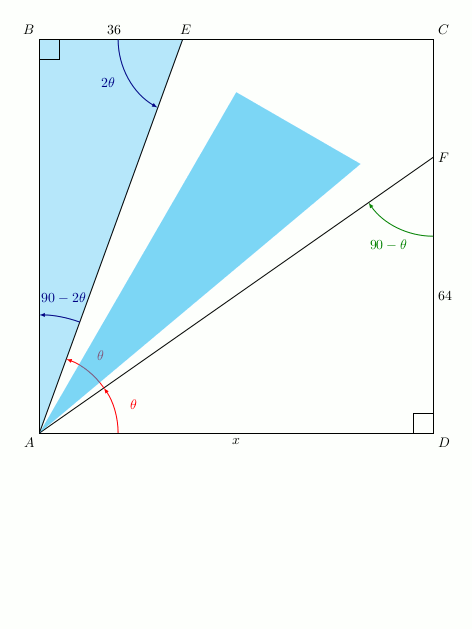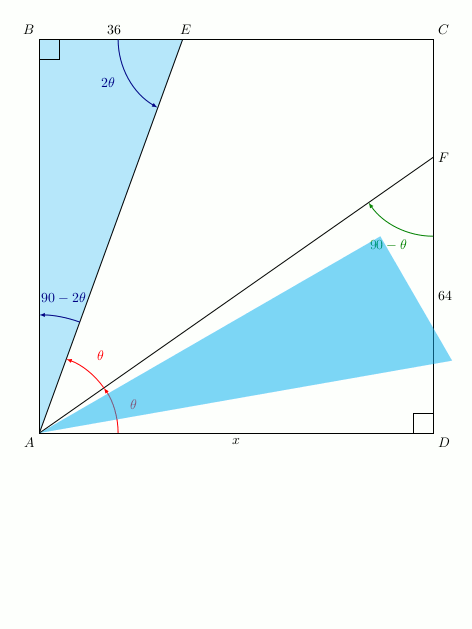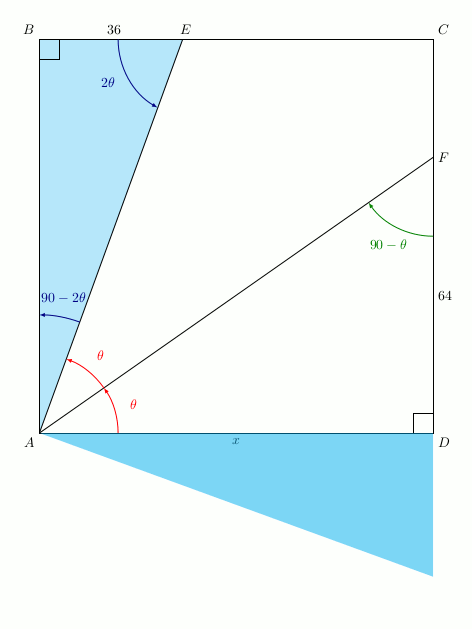
Notons \(\theta = \widehat{DAF} = \widehat{FAE}\) (car (AF) est la bissectrice de \(\widehat{DAE}\)).
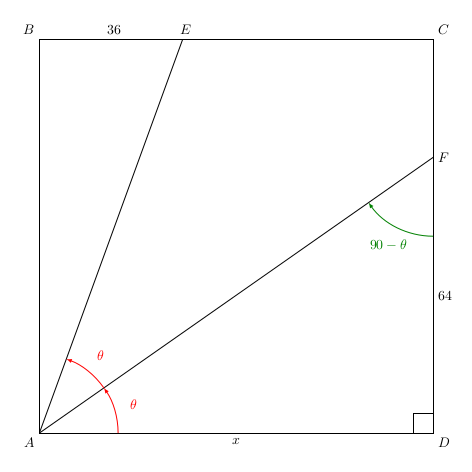
Le triangle FAD est rectangle en D donc les angles \(\widehat{FAD}\) et \(\widehat{DFA}\) sont complémentaires:$$\widehat{DFA}=90-\widehat{FAD}=90-\theta.$$On convient bien entendu que tous les angles sont exprimés en degrés.
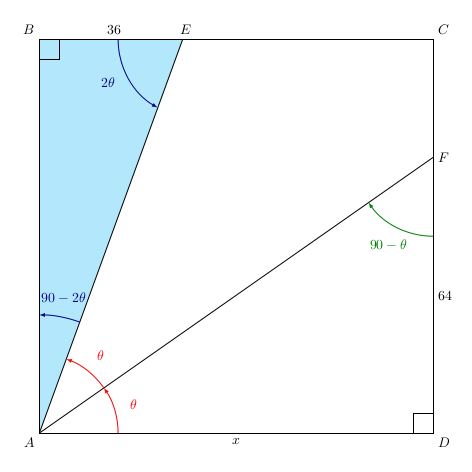
Les angles \(\widehat{DAE}\) et \(\widehat{EAB}\) sont adjacents et complémentaires donc: $$\widehat{EAB}=90-\widehat{DAE}=90-2\theta.$$ De plus, \(\widehat{BEA}=\widehat{DAE}\) car ils sont alternes-internes formés par deux droites parallèles : (AD) et (BC).
Faisons donc une rotation de centre A et d’angle \(2\theta\) dans le sens des aiguilles d’une montre:
On obtient:
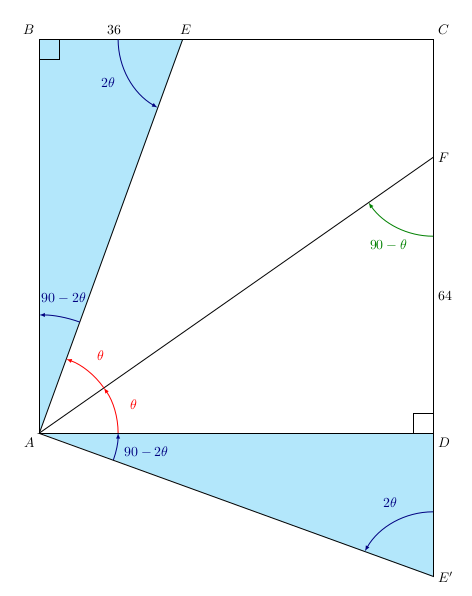
Notons E’ l’image de E par cette rotation. Si l’on regarde l’angle \(\widehat{E’AF}\), sa mesure vaut \(90-2\theta+\theta=90-\theta\):
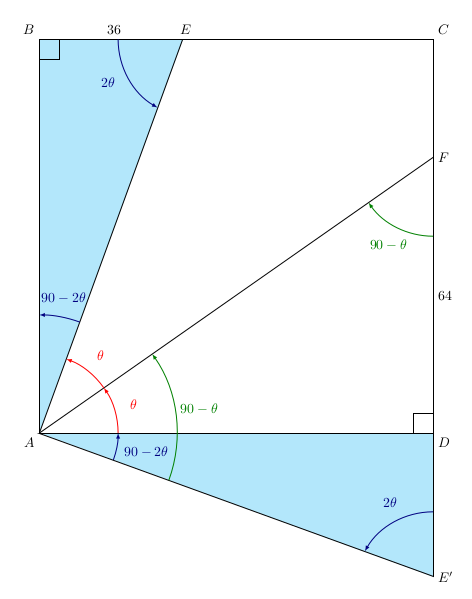
Ainsi, dans le triangle E’AF, les angles \(\widehat{E’AF}\) et \(\widehat{E’FA}\) ont la même mesure:
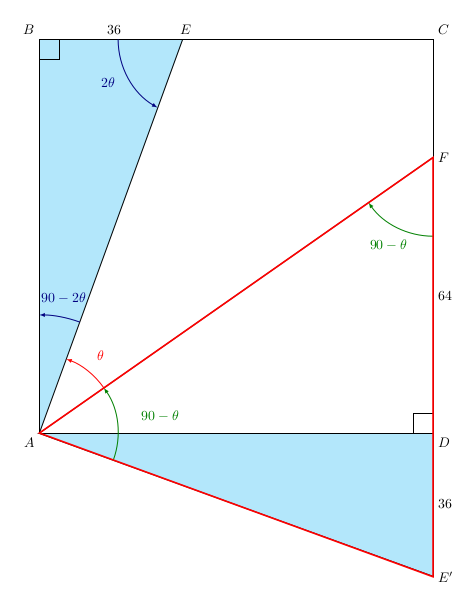
Ce triangle est donc isocèle en E’; ainsi E’A = E’F.
Or, E’A = EA car une rotation conserve les longueurs (rappelons que [E’A] est l’image de [EA] par la rotation considérée).
Ainsi, EA = E’A = E’F = 36 + 64 = 100.
Autres approches
Ce problème est exposé dans la vidéo de la chaîne MindYourDecisions suivante, où l’on y expose d’autres approches plus compliquées, dont une qui mène à une équation de degré 2, mais en faisant intervenir des tangentes et une relation sur les tangentes qui n’est pas un programme du lycée en France.
Les fichiers sources \(\LaTeX\) des figures sont disponibles ci-dessous pour les abonné·e·s de mathweb.fr :


