Sur cette page, nous allons voir une méthode pour déterminer une valeur approchée de la longueur d’une courbe représentative d’une fonction sur un intervalle donné en Python.

Approche mathématique
Une courbe peut être vue comme une succession de segments minuscules. Prenons cette courbe:
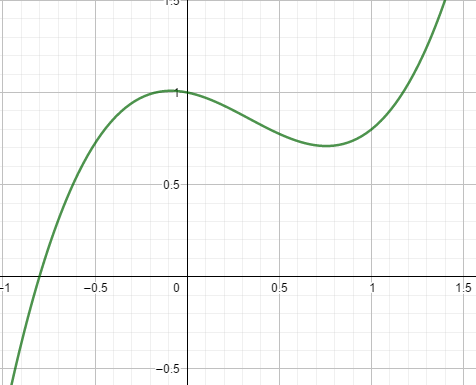
Divisons l’intervalle [-0,5 ; 1] en 3 par exemple:
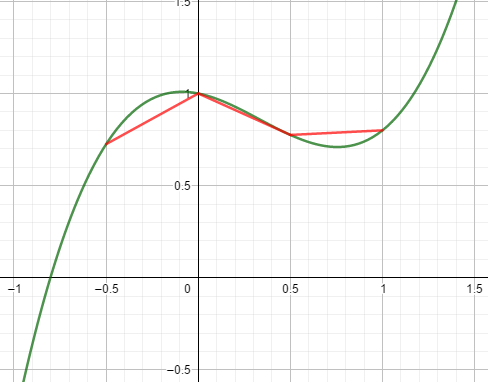
On a ici tracé 3 segments; certes, ils ne « collent » pas à la courbe, mais on peut imaginer que si l’on divise l’intervalle [-0,5 ; 1] en plus de 3, les segments vont être très petits et donc vont coller à la courbe. La longueur totale de ces segments va donc être très proche de la longueur de la courbe.
Longueur d’une portion de courbe en Python
Nous allons avant tout définir une fonction Python qui représente la fonction mathématique \(f(x)=x^3-x^2-0,2x+1\) dont la courbe représentative est donnée précédemment.
def f(x):
return x**3 - x**2 - 0.2*x +1Ensuite, nous créons une fonction Python longueur(a,b,n) qui admet 3 arguments : a et b sont les bornes de l’intervalle, et n le nombre de subdivisions souhaitées (le nombre de segments à considérer).
def longueur(a,b,n):
pas = (b - a) / n
x = a
longueur = 0
while x <= b-pas:
longueur += ( pas**2 + ( f(x+pas) - f(x) )**2 )**0.5
x += pas
return longueurOn commence par définir le pas, c’est-à-dire la longueur des subdivisions de l’intervalle [a ; b] : c’est la longueur de l’intervalle que l’on a divisé par n (→ ligne 5).
Ensuite, on part de x = a (→ ligne 6) et on initialise la longueur à 0 (→ ligne 7). Nous allons parcourir l’intervalle par petits sauts : x, puis x + pas, puis x + 2pas, etc.
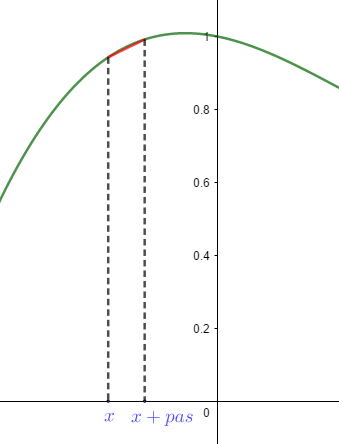
Pour un x donné, on calcule la longueur du segment entre x et x + pas à l’aide de la formule:$$AB = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}$$qui donne dans notre cas:$$\sqrt{(x+pas-x)^2+(f(x+pas)-f(x))^2}=\sqrt{pas^2+(f(x+pas)-f(x))^2}.$$C’est ainsi que l’on obtient la ligne 9 : on ajoute à la longueur le nombre calculé.
Ce calcul est fait jusqu’à ce que x soit égal à b – pas. Ensuite, la boucle while s’arrête et la fonction Python retourne la dernière valeur de longueur calculée, qui correspond donc à la somme des longueurs des segments.
En exécutant ce programme, on a par exemple:
>>> longueur(-0.5,1,100) 1.674759304224313 >>> longueur(-0.5,1,1000) 1.693754517038786 >>> longueur(-0.5,1,10000) 1.6937551333505372
N’oubliez pas que si vous avez des difficultés en mathématiques, je peux vous aider par webcam !
[Retour aux ressources Python]