Graphique en Python: matplotlib vs LaTeX. Je ne sais pas pour vous, mais de mon côté, j’ai de gros problèmes avec matplolib, le module de Python. Je trouve que les résultats sont bien dégueux… Heureusement, \(\LaTeX\) est mon ami !
Graphique en Python: matplotlib vs LaTeX – Introduction
Comme je m’ennuie lamentablement aujourd’hui, j’ai souhaité construire un nuage de points représentatif de l’évolution du nombre de visites uniques sur mon site mathweb.fr.
Je me suis donc aidé des statistiques depuis 2 mois et j’ai reporté les nombres de visites dans un tableur que j’ai ensuite converti en fichier CSV afin d’exploiter les données.
Mais j’ai été horrifié par le résultat du code suivant:
from matplotlib.pylab import plot,show
file = "C:\\Users\\Stephane\\Mes Documents\\MATHWEB\\stats.csv"
days, dates , visits = [] , [] , []
with open(file , 'r' , encoding='utf8') as f:
lines = f.readlines()
n = len( lines )
for l in lines:
temp = l.split(',')
days.append( temp[2].replace('\n','') )
dates.append( temp[0] )
visits.append( int(temp[1]) )
plot(visits)
show()
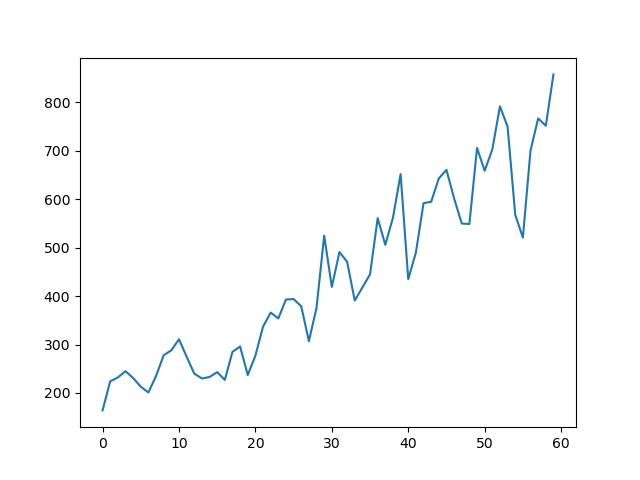
Comme je trouve ça assez moche, je me suis dit qu’il fallait que je fasse un graphique en \(\LaTeX\). Seul un physicien pourrait se contenter de cette merde… 🙂 Bah ! Je plaisante ! (j’aime bien taquiner les physiciens…)
Graphique en Python: matplotlib vs LaTeX – Construction du graphique en \(\LaTeX\)
Graphique en Python: matplotlib vs LaTeX – Les dimensions et les échelles
On va commencer par fixer les dimensions et les échelles.
# valeur maximale en ordonnée max_y = ((max(visits)//100)+1)*100 # échelles en abscisse et en ordonnée scale_x = 1/3 scale_y = 1/50 # dimension du document PDF paperheight = (max_y * scale_y + 1) * 10 # en mm paperwidth = (n * scale_x + 1) * 10 # en mm
Les échelles sont arbitraires… Pour un plus grand nombre de valeurs (je n’en ai que 60), je choisirai une échelle plus petite que 1/3 pour les abscisses.
Le document \(\LaTeX\)
Bon, là, c’est ennuyant donc je ne vais pas détailler le code (le fichier source est de toute manière disponible pour les abonné·e·s de mathweb.fr).
Mais l’idée est de construire une variable, que j’ai appelée « document » qui est une chaîne de caractères contenant le code \(\LaTeX\) de mon graphique.
Quand je lance le programme, voici ce qui se passe:
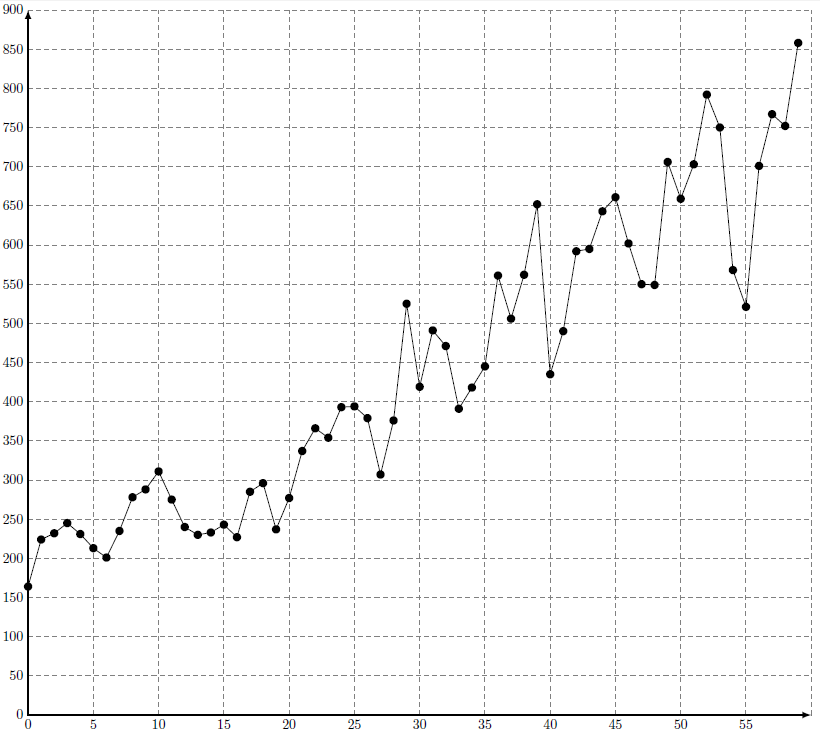
Il faut bien admettre que le résultat est bien plus convainquant que celui de matplotlib non ?
Prévisions
Ce que j’aimerais faire maintenant, c’est une prévision du nombre de visites pour l’avenir. Constatant que la progression est exponentielle, je vais considérer le logarithme népérien des nombres de visites pour faire une régression linéaire.
xx = range(n) yy = [ log(visits[i]) for i in xx ] a,b = polyfit(xx , yy , 1) plot(xx , yy , "o") plot(xx , a*xx+b) show()
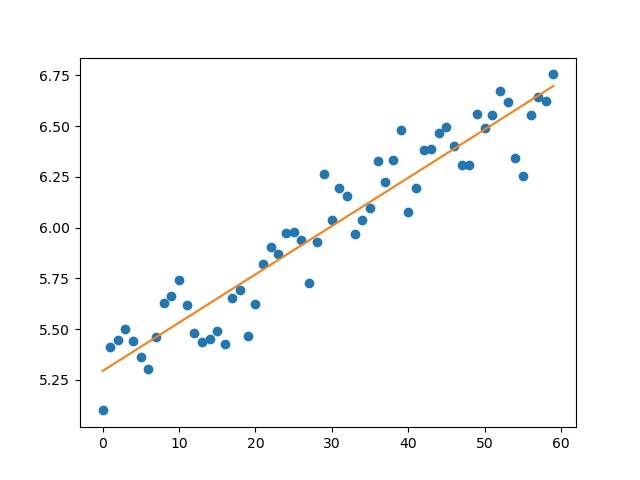
En affichant les valeurs de a et b, on a l’équation de droite suivante:$$y=0.023790612870157827x + 5.293931301639233.$$
Cela signifie que:$$\ln(N)=0.023790612870157827x + 5.293931301639233$$et donc:$$N=\text{e}^{0.023790612870157827x + 5.293931301639233}.$$
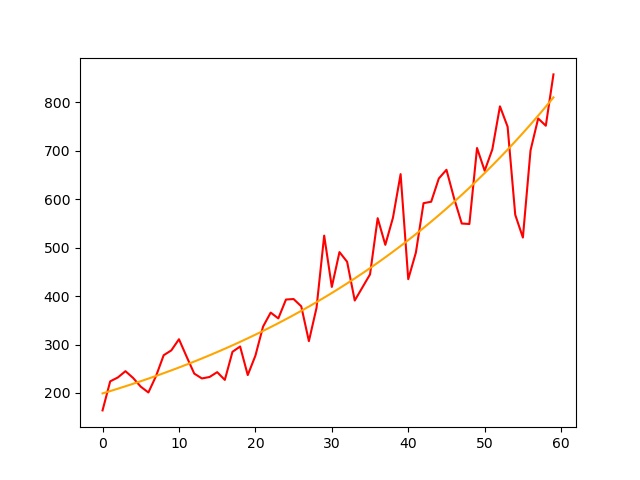
Cette estimation sera-t-elle correcte ? Nous verrons à Noël… Car selon ce modèle, à cette période, il devrait y avoir 4388 visites ! Je ne sais pas pourquoi, mais je pense que ce modèle est erroné…


