En mathématiques, l’adjectif « canonique » sous-entend « plus simple » (pour effectuer certaines opérations).
Il est souvent introduit pour une certaine forme des polynômes du second degré en lycée, mais il peut aussi qualifier des formes d’autres fonctions.

Les polyômes de degré 2

Un polynôme de degré 2 est un polynôme de la forme : \[ ax^2+bx+c\qquad,\qquad a\neq0.\]

En factorisant par a, on obtient : \[ a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right).\]

Ici, l’idée plutôt astucieuse est de voir \(\displaystyle x^2+\frac{b}{a}x\) comme le début du développement de \(\displaystyle\left(x+\frac{b}{2a}\right)^2\). En effet,\[\left(x+\frac{b}{2a}\right)^2=x^2+\frac{b}{a}x+\frac{b^2}{4a^2}.\]

Ainsi, on peut écrire : \[ \begin{align*}a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)&=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a^2}+\frac{c}{a} \right]\\&=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a^2} \right].\end{align*}\]

C’est cette dernière expression que l’on nomme forme canonique du polynôme \(ax^2+bx+c\).

Cette expression est jugée plus « simple » que la première car elle permet :

1. de trouver les racines du polyôme : en effet, résoudre l’équation \(ax^2+bx+c=0\) directement n’est pas chose aisée alors que résoudre l’équation \(\displaystyle a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a^2} \right]\) l’est un peu plus. En effet, \[ \begin{align*}a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a^2} \right]=0 & \iff\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a^2}=0 \text{ (car }a\neq0)\\ & \iff \left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}\end{align*} \] En notant : \[ \Delta = b^2-4ac \qquad \text{(on appelle ce nombre le }discriminant)\]
   • si \(\Delta<0\), alors l’équation n’a pas de solution ;
   • si \(\Delta=0\), alors \(\displaystyle x+\frac{b}{2a}=0\), soit \(\displaystyle x=-\frac{b}{2a}\) ;
   • si \(\Delta>0\), alors il y a deux solutions réelles qui sont : \[ \alpha=\frac{-b-\sqrt{\Delta}}{2a}\qquad\text{et}\qquad\beta=\frac{-b+\sqrt{\Delta}}{2a}.\]
2. de trouver le signe du polynôme :
   • si \(\Delta<0\), on ne peut pas factoriser la forme canonique plus qu’elle ne l’est déjà et \(\displaystyle\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a^2}>0\) donc le polynôme est du signe de « a » sur \(\mathbb{R}\) ;
   • si \(\Delta=0\), la forme canonique se réduit à \(\displaystyle a\left(x+\frac{b}{2a}\right)^2\), et comme un carré est toujours positif ou nul, elle sera du signe de « a » sur \(\mathbb{R}\) sauf pour \(\displaystyle x=-\frac{b}{2a}\) où elle sera nulle ;
   • si \(\Delta>0\), \(ax^2+bx+c=a(x-\alpha)(x-\beta)\), où \(\alpha\) et \(\beta\) sont les deux racines. \(x-\alpha>0\) pour \(x>\alpha\) et \(x-\beta>0\) pour \(x>\beta\) donc en admettant que \(\alpha<\beta\), on aura : où « sgn(a) » désigne le signe de a  et « sgn(-a) » désigne le signe opposé à a.
3. de montrer que la représentation graphique admet un extremum :  en effet, pour tout réel x, \[ \left(x+\frac{b}{2a}\right)^2\geq 0 \] donc : \[ \left(x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\geq-\frac{\Delta}{4a^2}\;. \] Ainsi, \[ \begin{align*}a\left[\left(x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right]\geq-\frac{\Delta}{4a}\qquad\text{si }a>0.\\\text{ Dans ce cas, la courbe a un minimum.}\\ a\left[\left(x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right]\leq-\frac{\Delta}{4a}\qquad\text{si }a<0.\\\text{ Dans ce cas, la courbe a un maximum.}\end{align*}\] Notons que cet extremum est atteint pour \(\displaystyle x=-\frac{b}{2a}\) (la valeur de x qui annule le carré).
4. de montrer que la courbe représentative du polynôme de degré 2 admet un axe de symétrie d’équation \(\displaystyle x=-\frac{b}{2a}\). Pour cela, on calcule \(\displaystyle f\left(-\frac{b}{2a}+x\right)\) et \(\displaystyle f\left(-\frac{b}{2a}-x\right)\), où \( \displaystyle f(x)=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right]\) :
   • On a d’une part : \[ \begin{align*}
     f\left(-\frac{b}{2a}+x\right) & = a\left[\left(-\frac{b}{2a}+x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right]\\ & = a\left[x^2-\frac{\Delta}{4a^2}\right]. \end{align*}\]
   • On a d’autre part : \[ \begin{align*}f\left(-\frac{b}{2a}-x\right) & = a\left[\left(-\frac{b}{2a}-x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right]\\& = a\left[x^2-\frac{\Delta}{4a^2}\right].\end{align*}\]

   On voit donc ici que \(\displaystyle f\left(-\frac{b}{2a}-x\right)=f\left(-\frac{b}{2a}+x\right)\), ce qui prouve que la droite d’équation \(\displaystyle x=-\frac{b}{2a}\) est un axe de symétrie de la courbe représentative de f.

Les fonctions homographiques

Ce sont les fonctions de la forme : \[ \frac{ax+b}{cx+d}\qquad,\qquad a\neq0,\ c\neq0. \]

En factorisant par a au numérateur et par c au dénominateur, on obtient : \[ \frac{a\left(x+\frac{b}{a}\right)}{c\left(x+\frac{d}{c}\right)}=\frac{a}{c}\times\frac{x+\frac{b}{a}}{x+\frac{d}{c}}. \]

L’idée ici est de faire apparaître le dénominateur au numérateur : \[ \frac{a}{c}\times\frac{x+\frac{d}{c}+\frac{b}{a}-\frac{d}{c}}{x+\frac{d}{c}}\]

pour ensuite « couper » la fraction en deux : \[ \frac{a}{c}\left(\frac{x+\frac{d}{c}}{x+\frac{d}{c}}+\frac{\frac{b}{a}-\frac{d}{c}}{x+\frac{d}{c}} \right)=\frac{a}{c}\left(1+\frac{\frac{bc-ad}{ac}}{x+\frac{d}{c}}\right).\]

Cette dernière expression est la forme canonique de la fonction homographique.

Elle permet :

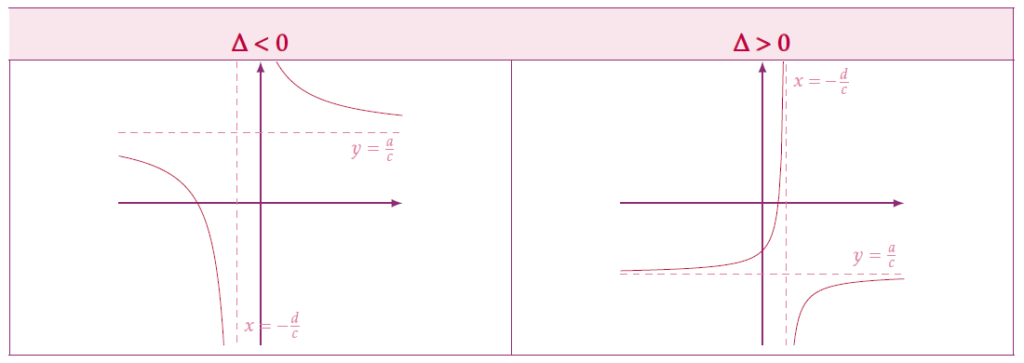
1. de voir que la représentation graphique de la fonction homographique admet une asymptote horizontale : en effet, le terme \(\displaystyle\frac{\frac{bc-ad}{c^2}}{x+\frac{d}{c}}\) se rapproche de 0 lorsque x prend des valeurs de plus en plus grandes (on dit que la limite de ce terme est égale à 0 quand x tend vers \(+\infty\)). Donc, \(\displaystyle\frac{ax+b}{cx+d}\) va se rapprocher de la valeur \(\displaystyle\frac{a}{c}\) au voisinage de \(+\infty\) (et même au voisinage de \(-\infty\), le raisonnement étant le même). La droite d’équation \(y=\frac{a}{c}\) sera donc asymptote à la courbe représentative de notre fonction.
2. de trouver le sens de variation de la fonction sur chaque intervalle de son domaine de définition. En effet, le domaine de définition de la fonction homographique est \(\mathcal{D}_f=\left]-\infty~;~-\frac{d}{c}\right[\cup\left]-\frac{d}{c}~;~+\infty\right[\). Plaçons-nous sur l’un des deux intervalles.
   • La fonction \( x\mapsto x+\frac{d}{c}\) est affine de coefficient directeur positif, donc elle est croissante sur l’intervalle considéré.
   • La fonction \(x\mapsto\frac{1}{x}\) est décroissante sur \(]0;+\infty[\) et sur \(]-\infty;0[\) donc \(x\mapsto\frac{1}{x+\frac{d}{c}}\) est décroissante sur l’intervalle considéré.
     • Si \(bc-ad>0\), \(x\mapsto\frac{\frac{bc-ad}{c^2}}{x+\frac{d}{c}}\) est décroissante (car on ne change pas le sens de variation d’une fonction en la multipliant par un nombre positif). Et donc, \(x\mapsto\frac{a}{c}+\frac{\frac{bc-ad}{c^2}}{x+\frac{d}{c}}\) aussi.
     • Si \(bc-ad<0\), \(x\mapsto\frac{\frac{bc-ad}{c^2}}{x+\frac{d}{c}}\) est croissante (car on change le sens de variation d’une fonction en la multipliant par un nombre négatif). Ainsi, \(x\mapsto\frac{a}{c}+\frac{\frac{bc-ad}{c^2}}{x+\frac{d}{c}}\) est aussi croissante.

   À partir de ces observations, on peut poser :\[ \Delta=ad-bc\] et dire :

   • si \(\Delta<0\), la fonction est décroissante sur chaque intervalle de son domaine de définition ;
   • si \(\Delta>0\), la fonction est croissante sur chaque intervalle de son domaine de définition.
3. de montrer que la courbe représentative de la fonction homographique a un centre de symétrie \(\displaystyle\Omega\left(-\frac{d}{c}~;~\frac{a}{c}\right)\). Si on note \(\displaystyle f(x)=\frac{a}{c}+\frac{\frac{bc-ad}{c^2}}{x+\frac{d}{c}}\), on calcule \(f(x_\Omega+x)+f(x_\Omega-x)\) : \[ \begin{align*} f\left(-\frac{d}{c}+x\right)+f\left(-\frac{d}{c}-x\right) & = \frac{a}{c}+\frac{\frac{bc-ad}{c^2}}{x}+\frac{a}{c}+\frac{\frac{bc-ad}{c^2}}{-x}\\ & = 2\frac{a}{c}\\f(x_\Omega+x)+f(x_\Omega-x)& = 2y_\Omega. \end{align*} \] Cela prouve bien que \(\Omega\) est le centre de symétrie de la courbe. 

Les sources \(\LaTeX\) du document PDF: