Giulio Fagnano était un mathématicien italien de la fin du XVIIe siècle.
Il a probablement été le premier à s’être intéressé à la théorie des intégrales elliptiques, mais ce n’est pas l’objet de cet article.
Le problème connu sous le nom de problème de Fagnano est le suivant :
Peut-on inscrire un triangle de périmètre minimal dans un triangle acutangle ?
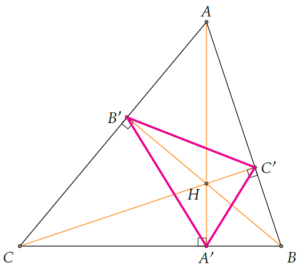
Le triangle orthique
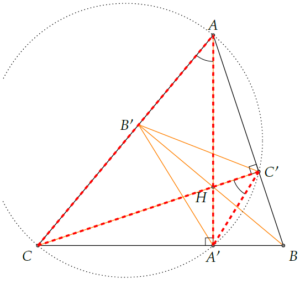
Le triangle orthique du triangle ABC est le triangle A’B’C’, dont les sommets sont les pieds des hauteurs de ABC.
Maintenant, vous allez sans doute me demander le rapport entre le triangle orthique et le problème de Fagnano, n’est-ce pas ?
Et bien, on peut démontrer que le triangle solution au problème de Fagnano est le triangle orthique du triangle donné.
Voyons cela dans la section suivante…
La solution au problème de Fagnano
Considérons donc un triangle acutangle ABC.
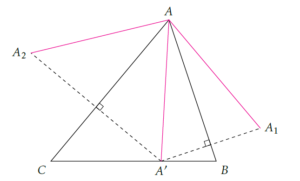
Dans un premier temps, on fixe A’ sur (BC), puis nous allons trouver les points B’ et C’, respectivement sur (AC) et (AB) de sorte que le périmètre de A’B’C’ soit la plus petite possible.
On va construire alors :
- \(A_1\) le symétrique de A’ par rapport à (AB) ;
- \(A_2\) le symétrique de A’ par rapport à (AC).
On a alors : \[ AA_2=AA’=AA_1 \qquad\text{et}\qquad \left\lbrace\begin{array}{l} \widehat{A’AB}=\widehat{A_1AB}\\\widehat{A’AC}=\widehat{A_2AC}\end{array}\right.\]
car les triangles \(AA’A_2\) et \(AA’A_1\) sont isocèles en A.
Notons : \[ \gamma = \widehat{BAC}\quad\text{exprimé en degrés}.\]
Alors, \[ \widehat{A_1AA_2}=2\gamma.\]
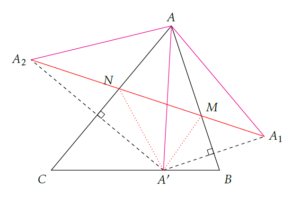
Le triangle ABC étant acutangle, \(0<\gamma<90\) donc \(0<2\gamma<180\). Ainsi, \((A_1A_2)\) coupe (AC) et (AB). Notons M et N les points d’intersection comme indiqués sur la figure ci-dessous :
Les triangles \(A’NA_2\) et \(A’MA_1\) sont isocèles respectivement en N et M. Donc, \[ NA_2=NA’\qquad\text{et}\qquad MA_1=MA’.\]
Ainsi, le périmètre de MNA’ est égal à \(A_1A_2\).
Si on considère M’ sur (AB) et N’ sur (AC), respectivement distincts de M et N, alors le périmètre de M’A’N’ est égal à la longueur de la ligne brisée \(A_2N’A’M’A_1\) pour les mêmes raisons que précédemment.
C’est bien connu : le chemin le plus court est la ligne droite donc la ligne brisée (bleue) est nécessairement de longueur supérieure à la longueur de \([A_1A_2]\).
Dans un deuxième temps, on cherche la position de A’ sur (BC).
Pour minimiser le périmètre du triangle A’MN, on doit donc trouver la position de A’ sur (BC).
Comme nous l’avons vu, ce périmètre vaut \(A_1A_2\), où \([A_1A_2]\) est la base du triangle isocèle \(AA_1A_2\) dont l’angle au sommet principal est constant et vaut toujours \(2\gamma\).
Pour minimiser \(A_1A_2\), il faut minimiser \(AA_1\), soit AA’ car ces deux longueurs sont égales.
Or, la distance la plus courte entre un point (ici, A) et une droite (ici, (BC)) est la longueur du segment perpendiculaire à la droite et passant par le point, donc ici la hauteur issue de A.
Ainsi, A’ est le pied de la hauteur du triangle ABC issue de A.
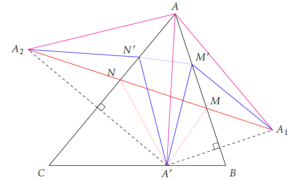
Dans un troisième temps, on montre que M = C’ et N = B’, où B’ et C’ sont respectivement les pieds des hauteurs de ABC issues de B et C.
Cette démonstration repose sur le fait que : \[ \widehat{BC’A’}=\widehat{BCA}\qquad\text{et}\qquad\widehat{BCA}=\widehat{AC’B’}.\qquad(1) \]
Alors, comme \(A’C’A_1\) est isocèle en C’, \[ \widehat{A_1C’B}=\widehat{BC’A’}=\widehat{BCA}=\widehat{AC’B’}\;,\]
ce qui signifie que B’, C’ et \(A_1\) sont alignés.
De la même façon, on montre que C’, B’ et \(A_2\) sont aussi alignés, ce qui finalement démontre que B’ et C’ sont sur la droite \(A_1A_2\) et donc que M = C’ et N = B’.
N.B. Les égalités (1) ne sont pas évidentes ; il faut donc les justifier.
Les triangles A’CA et C’CA sont rectangles d’hypoténuse [AC] ; donc [AC] est un diamètre du cercle \(\mathcal{C}\) passant par A, C, A’ et C’ comme l’illustre le schéma suivant :
Les angles \(\widehat{CAA’}\) et \(\widehat{CC’A’}\) interceptent le même arc \(\overparen{CA’}\) et sont inscrits dans le même cercle donc ils ont la même mesure : \[ \widehat{A’CA}=\widehat{CC’A’}\qquad(2)\]
De plus, le triangle A’CA est rectangle en A’ donc : \[ \widehat{CAA’}+\widehat{A’CA}=90^\circ.\]
Le triangle BCC’ est rectangle en C’ donc : \[ \widehat{CC’A’}+\widehat{A’C’B}=90^\circ.\]
Ainsi, \[ \widehat{A’C’B}+\widehat{CC’A’}=\widehat{CAA’}+\widehat{A’CA}\]
et donc, d’après l’égalité (2) : \[ \widehat{A’C’B}=\widehat{A’CA} \;,\]
ce qui démontre la première égalité des égalités (1).
L’angle \(\widehat{CA’C’}\) intercepte le petit arc \(\overparen{CC’}\) et l’angle \(\widehat{CAC’}=\widehat{BAC}\) intercepte le grand angle \(\widehat{CC’}\) ; ils sont donc supplémentaires.
De manière analogue, on démontre que \(\widehat{BA’B’}\) et \(\widehat{BAB’}=\widehat{BAC}\) sont aussi supplémentaires (en considérant les triangles rectangles AA’B et AB’B).
On obtient alors : \[ \widehat{BA’B’}=\widehat{CA’C’}\;,\]
ce qui montre que [A’A) est une bissectrice de l’angle \(\widehat{B’A’C’}\).
On peut démontrer de la même façon que [C’C) est une bissectrice de \(\widehat{A’C’B’}\), et donc que : \[ \widehat{AC’B’}=\widehat{BC’A’}\;,\]
soit : \[ \widehat{BCA}=\widehat{AC’B’}\;,\]
ce qui démontre la seconde égalité des égalités (1).
Obtenir les sources \(\LaTeX\) du document PDF: