Il y a de la suite dans les polygones réguliers… J’en veux pour preuve la réflexion qui m’est venue cette nuit… Étant donné un polygone régulier à n côtés, combien de diagonales possède-t-il ? Et en combien de morceaux ces diagonales le coupe-t-il ?
Tout au long de cet article, je vais noter:
- \(d_n\) le nombre de diagonales que possède un polygone régulier à \(n\) côtés;
- \(r_n\) le nombre de régions formées par ces diagonales à l’intérieur de ce polygone.
De la suite dans les polygones réguliers: observations préliminaires
Cas du carré
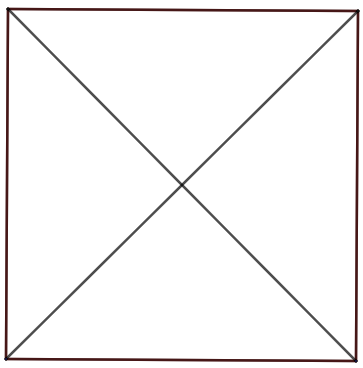
Nous avons ici:
- \(d_4=2\) (2 diagonales);
- \(r_4=4\) (4 régions formées à l’intérieur).
Cas du pentagone régulier
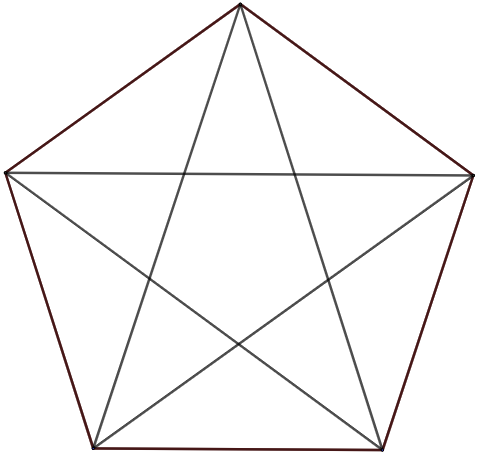
On a ici :
- \(d_5=5\)
- \(r_5=11\).
Cas de l’hexagone régulier
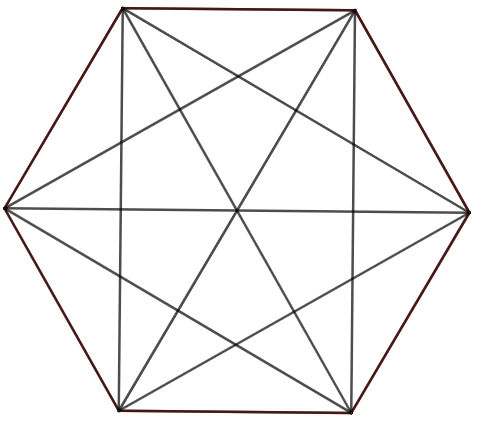
Ici,
- \(d_6=9\)
- \(r_6=24\)
Cas de l’heptagone régulier
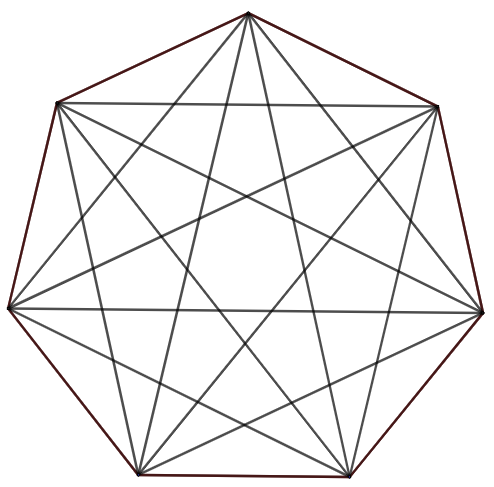
- \(d_7=14\)
- \(r_7=50\)
Cas de l’octogone régulier
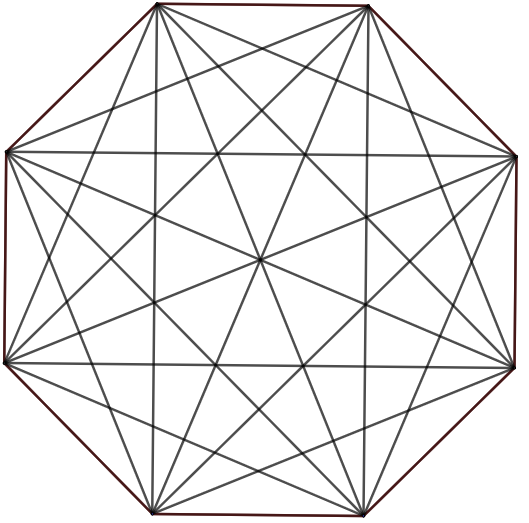
- \(d_8=20\)
- \(r_8=80\)
Cas de l’ennéagone (ou nonagone)
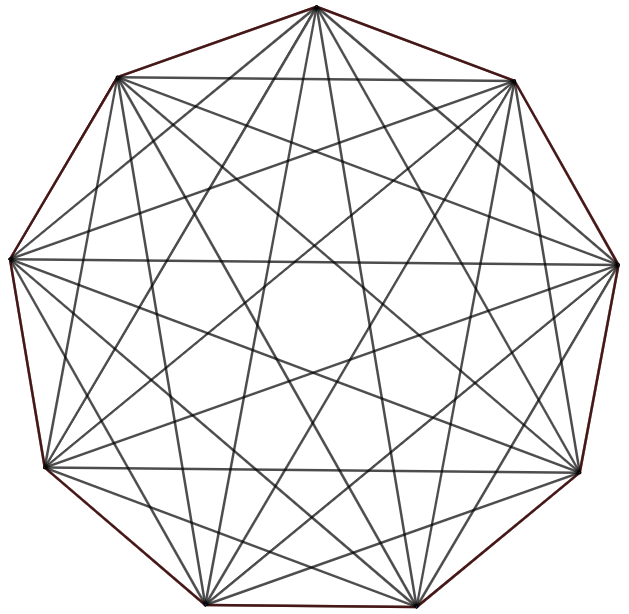
- \(d_9=27\)
- \(r_9=154\)
Je vais m’arrêter ici car autant compter les diagonales est facile, autant compter les régions l’est bien moins !
De la suite dans les polygones réguliers: nombre de diagonales
On peut s’aider des graphiques; pour :
- le pentagone, 2 diagonales partent de chaque sommet;
- l’hexagone, 3 diagonales partent de chaque sommet;
- l’heptagone, 4 diagonales partent de chaque sommet;
- l’octogone, 5 diagonales partent de chaque sommet;
- l’ennéagone, 6 diagonales partent de chaque sommet.
Nul besoin d’être sorti·e de la cuisse de Jupiter pour conjecturer alors que : $$d_n=\frac{n(n-3)}{2}.$$ Et ban! Dans les dents !
Et la preuve ducon ?
Oui, il faut une preuve pour être convaincu·e de ce que l’on suppose…
Si un polygone possède n sommets, il est assez immédiat d’être convaincu·e du fait que chaque sommet peut-être relié aux n-1 autres. Or, de ses n-1 segments, 2 sont des côtés. Il ne reste plus que n-3 diagonales pour chaque sommet.
Or, parmi ses n-3 diagonales, il y en a la moitié qui son comptées en double. En effet, si \(S_i\) et \(S_j\) sont deux sommets non consécutifs, alors les segments \([S_iS_j]\) et \([S_jS_i]\) sont identiques.
Ainsi, le nombre de diagonales est bien égal à \(d_n=\frac{n(n-3)}{2}\).
De la suite dans les polygones réguliers: nombre de régions
Après quelques recherches, je me suis aperçu que d’autres personnes s’étaient intéressées à cela avant moi.
Ainsi, la suite donnant le nombre de régions figure sur cette page de The OEIS Foundation. Et cet article de Bjorn Poonen et Michael Rubinstein donne deux formules: une permettant d’obtenir le nombre de régions, l’autre le nombre d’intersections des diagonales.
Posons:$$\delta_n(m)=\begin{cases}1 & \text{si }m\equiv0\mod n\\0 & \text{sinon}\end{cases}$$Alors,$$\begin{align} r_n & = \frac{n^4−6n^3+ 23n^2−42n+ 24}{24}\\&+\frac{−5n^3+ 42n^2−40n−48}{48}\delta_2(n)\\&+\frac{−53n^2+ 310n}{12}\delta_6(n)+\frac{49n}{2}\delta_{12}(n)+32n\delta_{18}(n)\\&+19n\delta_{24}(n)-36n\delta_{30}(n)-50n\delta_{42}(n)-190n\delta_{60}(n)\\&-78n\delta_{84}(n)-48n\delta_{90}(n)-78n\delta_{120}(n)-48n\delta_{210}(n).\end{align}$$


