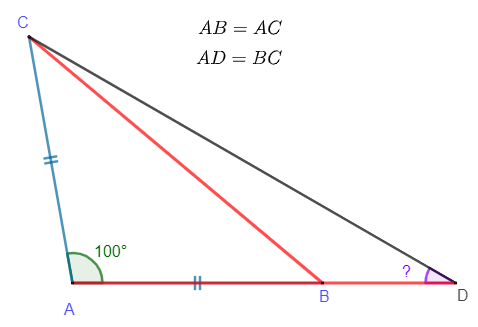
Étant donné un triangle ABC, isocèle en A et tel que \( \widehat{BAC}=100^\circ \), on considère un point D sur [AB) tel que AD = BC.
Il s’agit ici de déterminer la mesure de l’angle \( \widehat{ADC} \) sans consigne.
Une prise d’initiative: introduire un autre point
Il existe sans doute plusieurs méthodes, dont celle qui suit. Cette méthode peut être comprise dès le collège. Nous allons considérer le point E de sorte que ADE soit isocèle en E:
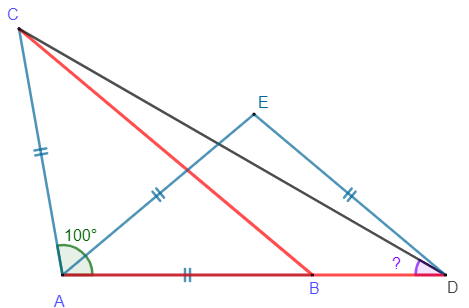
Étant isocèle en E, on peut facilement en déduire que \( \widehat{EAD} = \widehat{ADE} = 40^\circ \).
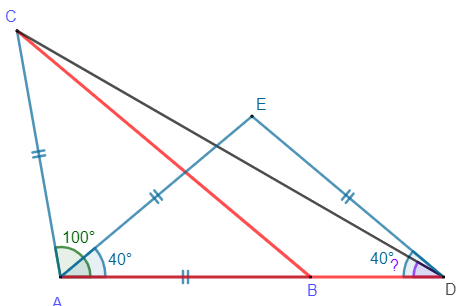
Ainsi, \( \widehat{EAC} = 60^\circ \). Comme le triangle EAC est isocèle en A, cela signifie qu’il est équilatéral.
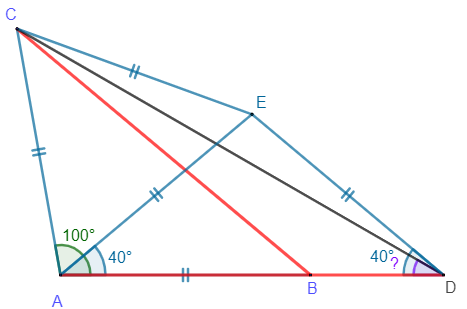
Le triangle CED est alors isocèle en E.
Le triangle ABC est isocèle en A avec \( \widehat{BAC} = 100^\circ \) donc \( \widehat{ABC} = \widehat{ACB} = 40^\circ \). Comme \( \widehat{ABD} \) est un angle plat, on en déduit que \(\widehat{DBC}=140^\circ\).
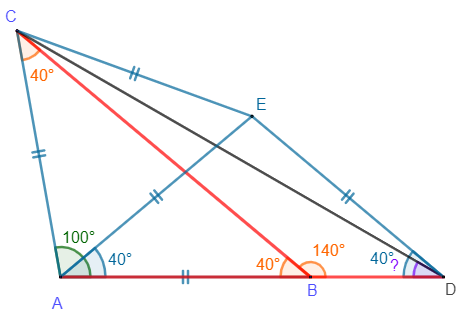
On en déduit alors que \( \widehat{BCE} = 20^\circ \) car, ne l’oublions pas, ACE est équilatéral et donc \(\widehat{ACE}=60^\circ\).
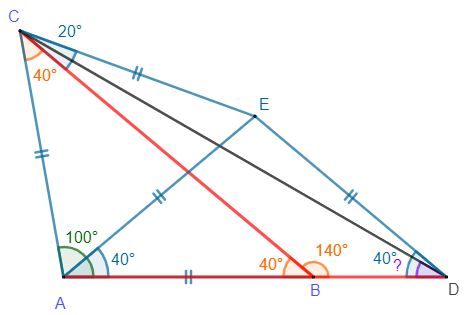
Dans le quadrilatère CEDB, la somme de la mesure des angles est égale à 360°. Cela signifie donc que \(\widehat{CED}=360-40-140-20=160^\circ\).
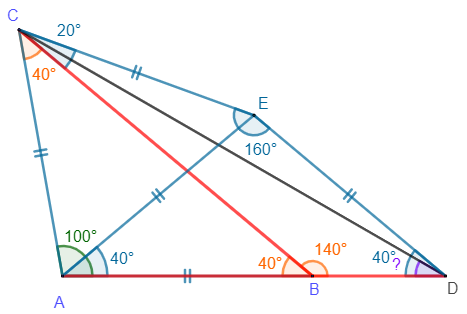
Le triangle CED étant isocèle en E, on en déduit que \(\widehat{ECD}=\widehat{EDC}=10^\circ\).
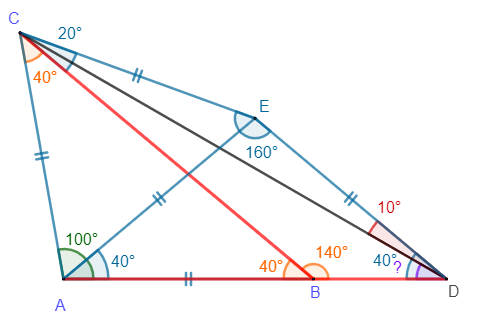
Ainsi, \( \widehat{ADC} = \widehat{ADE} – \widehat{EDC} = 40-10=30^\circ. \)
Les fichiers sources Géogebra
Ce problème a été traité dans la vidéo suivante:


