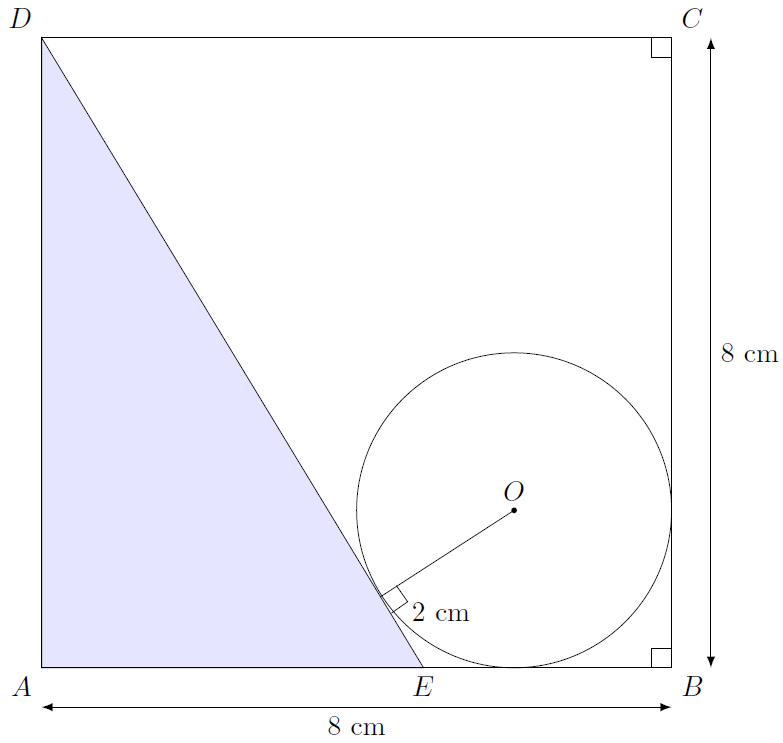
Nous allons aujourd’hui regarder comment déterminer l’aire du triangle bleu de la figure ci-dessous, de deux manières différentes.
Tout est parti de ce tweet :
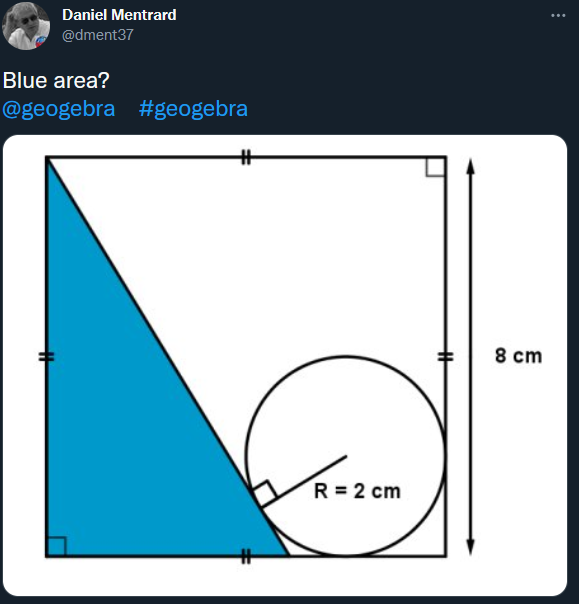
Comme j’ai du temps, je vais me pencher sur la question…
Le code LaTeX
\documentclass{standalone}
\usepackage{tikz}
\setlength{\parindent}{0pt}
\begin{document}
\begin{tikzpicture}
\filldraw[draw=black,fill=blue!10] (0,0) -- (0,8) -- (4.85,0) -- cycle;
\draw (0,0) rectangle (8,8);
\draw[<->,>=latex] (8.5,0) -- (8.5,8) node[midway,right] {8 cm};
\draw[<->,>=latex] (0,-.5) -- (8,-.5) node[midway,below] {8 cm};
\draw (6,2) circle (2cm);
\draw (7.75,0) -- (7.75,.25) -- (8,.25);
\draw (7.75,8) -- (7.75,7.75) -- (8,7.75);
\fill (6,2) circle (1pt) node[above] {$O$};
\draw (6,2) -- (4.3,0.9);
\begin{scope}[shift={(4.3,.9)},rotate=-55]
\draw (.25,0) -- (.25,.25) -- (0,.25) node[midway,below right] {2 cm};
\end{scope}
\node[below left] at (0,0) {$A$};
\node[below right] at (8,0) {$B$};
\node[above right] at (8,8) {$C$};
\node[above left] at (0,8) {$D$};
\node[below] at (4.85,0) {$E$};
\end{tikzpicture}
\end{document}
Aire du triangle: l’approche cartésienne
Je vais me placer dans le repère \( \big(A;\vec{AB},\vec{AD}\big)\).
Le point O a pour coordonnées (6;2) d’après l’énoncé donc son équation cartésienne est:$$(x-6)^2+(y-2)^2=4.$$
Cherchons le nombre m (non nul) tel que E(m ; 0) et (DE) tangente à ce cercle.
Le coefficient directeur de (DE) est \(-\frac{8}{m}\).
L’équation réduite de (DE) est donc:$$(DE)\quad:\quad y=-\frac{8}{m}x+8.$$
Cherchons maintenant les points d’intersection de (DE) et du cercle. Pour cela, on peut résoudre l’équation d’inconnue x:$$(x-6)^2+\left(-\frac{8}{m}x+8-2\right)^2=4 \iff (m^2+64)x^2-(12m^2+96m)x+68m^2=0$$
Nous voulons qu’il y ait une seule solution (afin que (DE) soit tangente au cercle) donc son discriminant doit être nul:$$(12m^2+96m)^2-4(m^2+64)\times68m^2=0.$$ soit: $$m^2(-128m^2+2304m-8192)=0.$$
Comme 0 < m < 8, on arrive alors à \( m = 9-\sqrt{17} \).
L’aire du triangle ADE est donc égale à :$$36-4\sqrt{17}\text{ cm}^2$$
Aire du triangle: l’approche euclidienne
\documentclass{standalone}
\usepackage{tikz}
\setlength{\parindent}{0pt}
\begin{document}
\begin{tikzpicture}
\filldraw[draw=black,fill=blue!10] (0,0) -- (0,8) -- (4.85,0) -- cycle;
\draw (0,0) rectangle (8,8);
\draw[<->,>=latex] (8.5,0) -- (8.5,8) node[midway,right] {8 cm};
\draw[<->,>=latex] (0,-.5) -- (8,-.5) node[midway,below] {8 cm};
\draw (6,2) circle (2cm);
\draw (7.75,0) -- (7.75,.25) -- (8,.25);
\draw (7.75,8) -- (7.75,7.75) -- (8,7.75);
\fill (6,2) circle (1pt) node[above] {$O$};
\draw (6,2) -- (4.3,0.9);
\begin{scope}[shift={(4.3,.9)},rotate=-55]
\draw (.25,0) -- (.25,.25) -- (0,.25) node[midway,below right] {2 cm};
\end{scope}
\node[below left] at (0,0) {$A$};
\node[below right] at (8,0) {$B$};
\node[above right] at (8,8) {$C$};
\node[above left] at (0,8) {$D$};
\node[below] at (4.85,0) {$E$};
\draw[thick,red] (0,8) -- (8,0);
\draw[thick,dashed,red] (0,2) node[left] {$F$} -- (6,2) node[midway,fill=white] {6 cm};
\draw[thick,red,shift={(0,8)}] (-45:1) arc (-45:-60:1);
\end{tikzpicture}
\end{document}
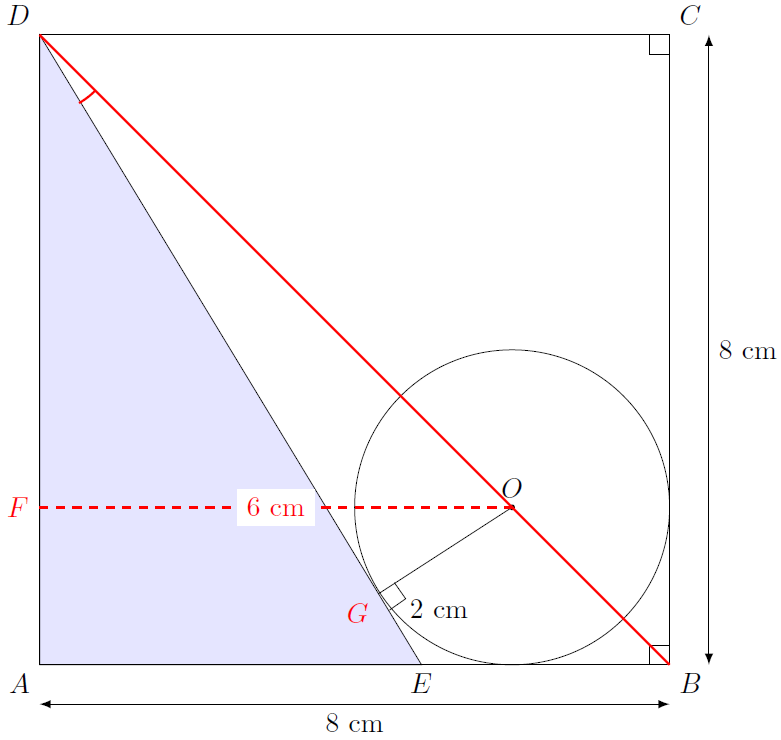
D’après le théorème de Pythagore appliqué dans le triangle FOD rectangle en F,$$DO=\sqrt{6^2+6^2}=6\sqrt{2}.$$
Dans le triangle DOG rectangle en G,$$DG=\sqrt{72-4}=\sqrt{68}=2\sqrt{17}.$$Donc,$$\widehat{ODG}=\arctan\left( \frac{\sqrt{17}}{17} \right).$$
Finalement,$$AE=8\tan\left[ \frac{\pi}{4}-\arctan\left(\frac{\sqrt{17}}{17}\right) \right]=8\times\frac{1-\tan\arctan\left(\frac{\sqrt{17}}{17}\right) }{1+\tan\arctan\left(\frac{\sqrt{17}}{17}\right) }$$et donc:$$AE=8\times\frac{1-\frac{\sqrt{17}}{17}}{1+\frac{\sqrt{17}}{17}}=9-\sqrt{17}.$$
Il vient alors que l’aire demandée est égale à \(4AE=36-4\sqrt{17}\).