Comment trouver la distance entre les centres des deux cercles ci-dessous ? ici, ces cercles sont tangents à la diagonale tracée ainsi qu’aux côtés du rectangle.
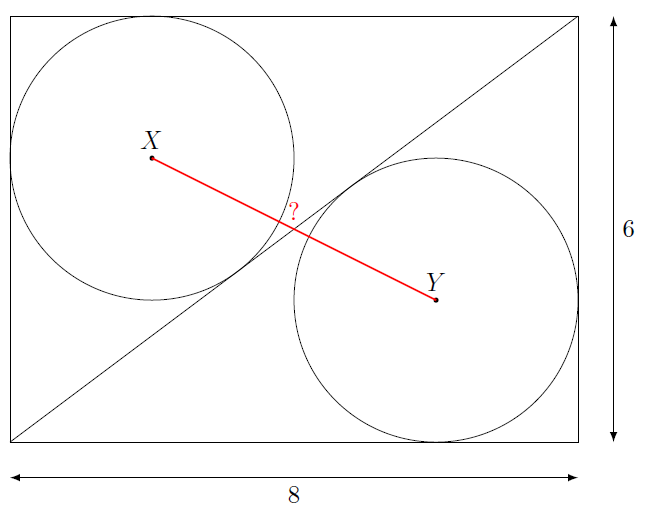
Distance entre les centres des deux cercles: calcul du rayon
Dans un premier temps, je vais calculer le rayon des deux cercles. Pour cela, je vais découper façon puzzle le demi-rectangle au-dessus de la diagonale en trois morceaux comme ci-dessous:
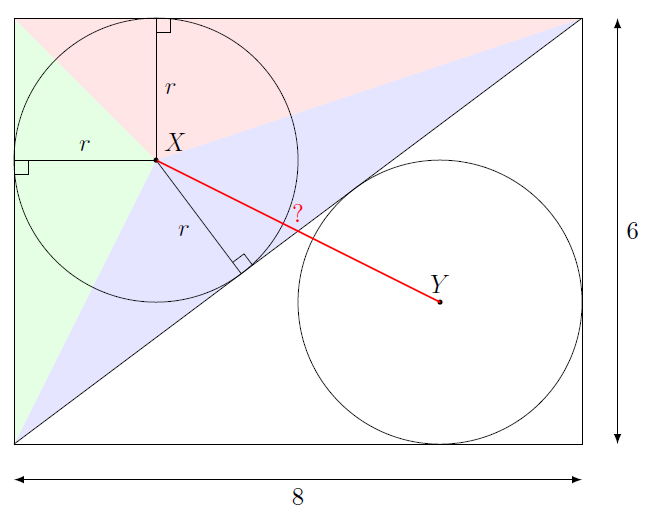
- L’aire du triangle bleu est: $$ \frac{\text{diagonale} \times r}{2} = \frac{10r}{2}=5r.$$
- De même, celle du triangle vert est: $$\frac{6r}{2}=3r$$et celle du triangle rouge est:$$\frac{8r}{2}=4r.$$
Ainsi, l’aire du demi-rectangle est la somme de ces trois aires, soit \(12r\).
Or, cette aire vaut \(\frac{8\times6}{2}=24\). On en déduit alors que:$$12r=24\quad\text{soit}\quad r=2.$$
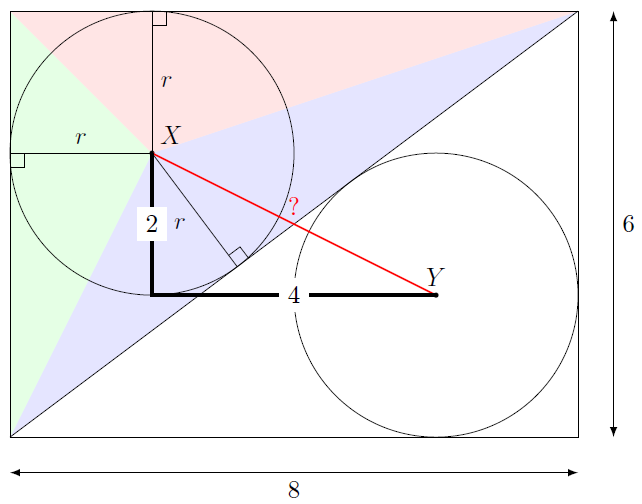
On en déduit alors que:$$XY=\sqrt{2^2+4^2}=\sqrt{20}=2\sqrt5.$$
Code LaTeX de la figure:
\documentclass{article}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\fill[blue!10] (0,0) -- (2,4) -- (8,6) -- cycle;
\fill[green!10] (0,0) -- (2,4) -- (0,6) -- cycle;
\fill[red!10] (0,6) -- (2,4) -- (8,6) -- cycle;
%
\draw (0,0) rectangle (8,6);
\draw (0,0) -- (8,6);
\draw (6,2) circle (2cm);
\draw (2,4) circle (2cm);
\fill (2,4) circle (1pt) node[above right] {$X$};
\fill (6,2) circle (1pt) node[above] {$Y$};
\draw[thick,red] (2,4) -- (6,2) node[midway,above] {?};
\draw[<->,>=latex] (8.5,0) -- (8.5,6) node[midway,right] {6};
\draw[<->,>=latex] (0,-.5) -- (8,-.5) node[midway,below] {8};
%
\draw (2,4) -- (3.2,2.4) node[midway,below left] {$r$};
\draw[shift={(3.2,2.4)},rotate=37] (.2,0) -- (.2,.2) -- (0,.2);
%
\draw (2,4) -- (0,4) node[midway,above] {$r$};
\draw (0,3.8) -- (.2,3.8) -- (.2,4);
%
\draw (2,4) -- (2,6) node[midway,right] {$r$};
\draw (2,5.8) -- (2.2,5.8) -- (2.2,6);
%
\draw[very thick] (2,4) -- (2,2) node[midway,fill=white] {2} -- (6,2) node[midway,fill=white] {4};
\end{tikzpicture}
\end{document}

