Il existe des résultats mathématiques au drôle de nom. Je vous expose ici ceux qui m’ont paru les plus drôles (pour un matheux… donc tout est à relativiser!).
Ces résultats mathématiques au drôle de nom: les théorèmes
Ces résultats mathématiques au drôle de nom: le théorème du toit
Soient deux plans sécants suivant une droite (d).
Si une droite est parallèle à ces deux plans alors elle est parallèle à (d).
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_du_toit
Le nom de ce théorème vient de la forme que prennent les deux plans sécants:

Ces résultats mathématiques au drôle de nom: le théorème des gendarmes
Dans un espace topologique E, étant donnés une partie A de E et un élément a de E adhérent à a, ainsi que trois fonctions f, g, et h de a dans \(\bar{\mathbb{R}}\) et un élément L de E,
si f ≤ g ≤ h et si \( \displaystyle\lim_{x\to a} f(x) = \lim_{x \to a} h(x) = L\) alors \(\displaystyle\lim_{x\to a} g(x)=L\).
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_gendarmes
Le véritable nom de ce théorème est le théorème d’encadrement, mais on lui donne plus souvent le nom de « théorème des gendarmes » car il est plus « imagé ».
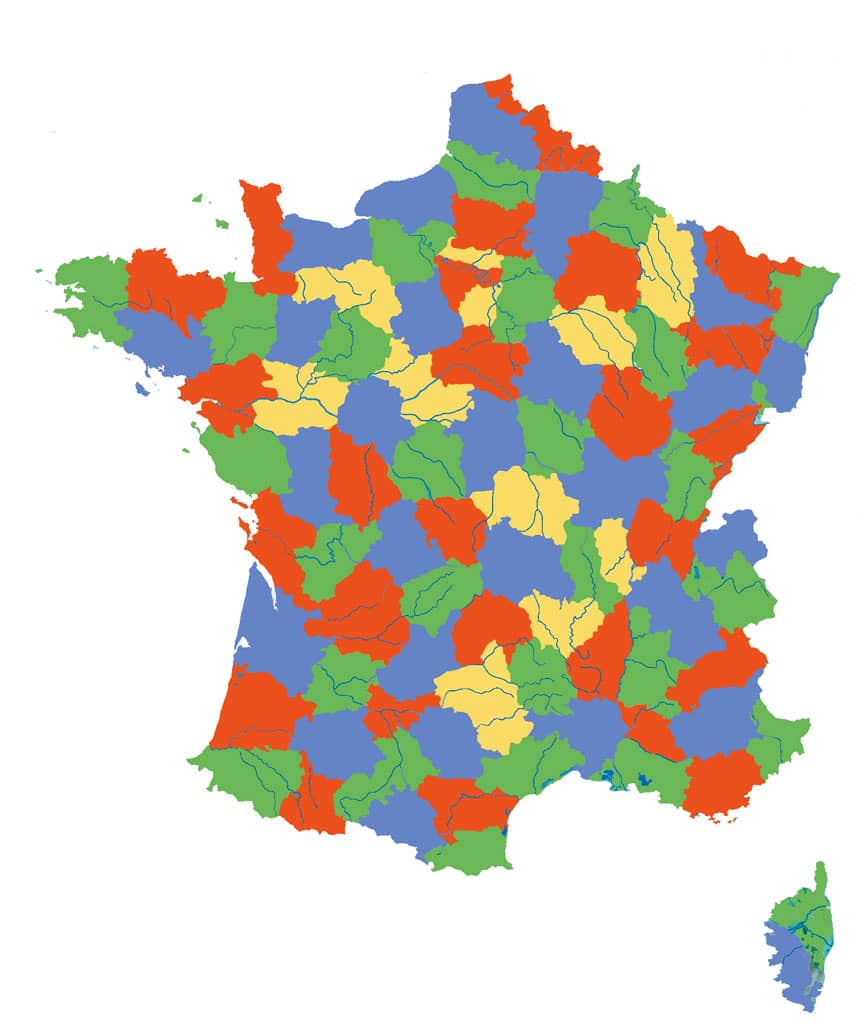
Le théorème des quatre couleurs
Quatre couleurs suffisent pour colorier n’importe quelle carte géographique sur Terre.
https://www.mathemathieu.fr/art/articles-maths/23-le-theoreme-des-quatre-couleurs
Théorème du rang
Soient E et F deux K-espaces vectoriels. Soit f une application linéaire de E dans F.
Alors, dim Im(f) + dim Ker(f) = dim(E).
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_du_rang
On appelle ce théorème ainsi car « dim Im(f) » est aussi appelé le « rang » de f.
Le théorème du sandwich au jambon
Il est possible de couper en quantités égales, d’un seul coup de couteau, le jambon, le fromage et le pain d’un sandwich.
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_du_sandwich_au_jambon
Autres résultats mathématiques
Lemme des bergers
Si un ensemble E possède une partition en p sous-ensembles contenant chacun r éléments, alors E contient p × r éléments.
https://fr.wikipedia.org/wiki/Lemme_des_bergers
Formule de Héron
Étant donné un triangle de côtés a, b et c, son aire est égale à \(\sqrt{p(p-a)(p-b)(p-c)}\), où \(p=\frac{a+b+c}{2}\).
https://fr.wikipedia.org/wiki/Formule_de_H%C3%A9ron
Le nom de cette formule ne vient pas de l’animal, mais du mathématicien Héron d’Alexandrie.
Le principe des tiroirs (de Dirichlet)
Si l’on dispose de n chaussettes et de m tiroirs, n > m, et si tous les tiroirs contiennent au moins une chaussette alors il existe un tiroir contenant au moins deux chaussettes.
https://fr.wikipedia.org/wiki/Principe_des_tiroirs
Je parlais dans un autre article de ce mathématicien: Les carrés de Dirichlet
Règle de l’Hôpital
Si f et g sont deux fonctions définies sur [a ; b[, dérivables en a, et telles que f(a) = g(a) = 0 et g′(a) ≠ 0 alors \(\displaystyle\lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)}\).
https://fr.wikipedia.org/wiki/R%C3%A8gle_de_L%27H%C3%B4pital


