Trouver le point du cercle pour lequel la distance totale est minimale

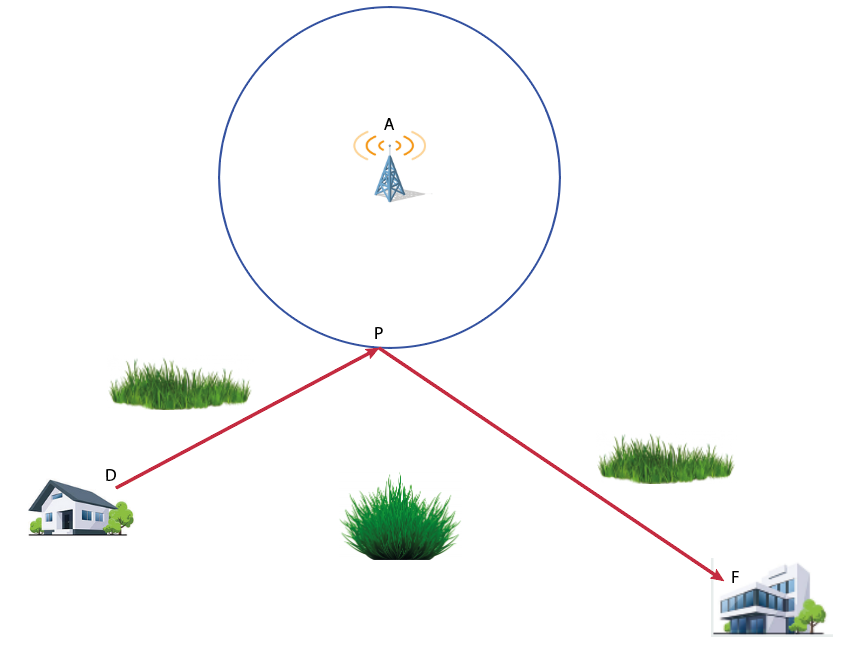
Je me trouve à mon domicile (D), en pleine campagne où il n’y a pas de réseau téléphonique.

Je dois me rendre chez mon ami Fabien (F), isolé lui aussi. Mais comme je suis une personne polie, je souhaite appeler Fabien afin de le prévenir de ma venue. Je dois donc me rendre au point (P) le plus proche possible de chez moi où il y a du réseau (donc sur le cercle de centre A, où A est l’antenne réseau) de sorte à minimiser la distance totale que je devrai parcourir (donc minimiser DP + PF).

La question est la suivante: où doit se trouver le point P ?

La recherche cartésienne: est-ce une bonne idée ?

Je vais simplifier le schéma et me rapporter à un repère orthonormé d’origine A.

Dans ce repère, le cercle a pour équation cartésienne:$$x^2+y^2=r^2,$où \(r\) est le rayon du cercle.

Je note maintenant:$$D(x_D;y_D)\quad;\quad F(x_F;y_F)$$les coordonnées respectives de D et F.

Je note \(P(x_P;y_P)\) tel que \(x_P^2+y_P^2=r^2\) puisque P appartient au cercle.

On a alors:$$DP=\sqrt{(x_P-x_D)^2 + (y_P-y_D)^2}\quad;\quad PF=\sqrt{(x_P-x_F)^2 + (y_P-y_F)^2}.$$

On cherche une condition sur \(x_P\) (par exemple) pour minimiser DP+PF. Cela n’équivaut pas à minimiser DP²+PF², donc nous sommes obligés de garder les racines carrées.

Notons:$$f(x,y)=\sqrt{(x-x_D)^2 + (y-y_D)^2} + \sqrt{(x-x_F)^2 + (y-y_F)^2}$$avec x²+y²=r². Alors,$$f(x,y)=\sqrt{r^2+x_D^2+y_D^2-2xx_D-2yy_D} + \sqrt{r^2+x_F^2+y_F^2-2xx_F-2yy_F}.$$

Comme \(y = \sqrt{r^2-x^2}\), on peut se ramener à une fonction à une variable:$$d(x)=f(x,y(x))=\sqrt{r^2+x_D^2+y_D^2-2xx_D-2y_D\sqrt{r^2-x^2}} + \sqrt{r^2+x_F^2+y_F^2-2xx_F-2y_F\sqrt{r^2-x^2}}.$$

Sa dérivée est:$$d'(x)=\frac{-x_D+\frac{y_Dx}{\sqrt{r^2-x^2}}}{\sqrt{r^2+x_D^2+y_D^2-2xx_D-2y_D\sqrt{r^2-x^2}}} + \frac{-x_F+\frac{y_Fx}{\sqrt{r^2-x^2}}}{\sqrt{r^2+x_F^2+y_F^2-2xx_F-2y_F\sqrt{r^2-x^2}}}.$$

Il faudrait trouver le signe de cette magnifique dérivée… mais cela semble plutôt ardu… L’approche cartésienne ne semble pas être la meilleure à envisager…

La recherche avec géogebra

Réalisons un schéma sur lequel nous allons placer un point P (que nous pourrons déplacer) sur le cercle.

Traçons les segments DP et PF, puis créons la variable a représentant la somme de ces distances. Bougeons ensuite P de sorte à rendre minimum cette somme.

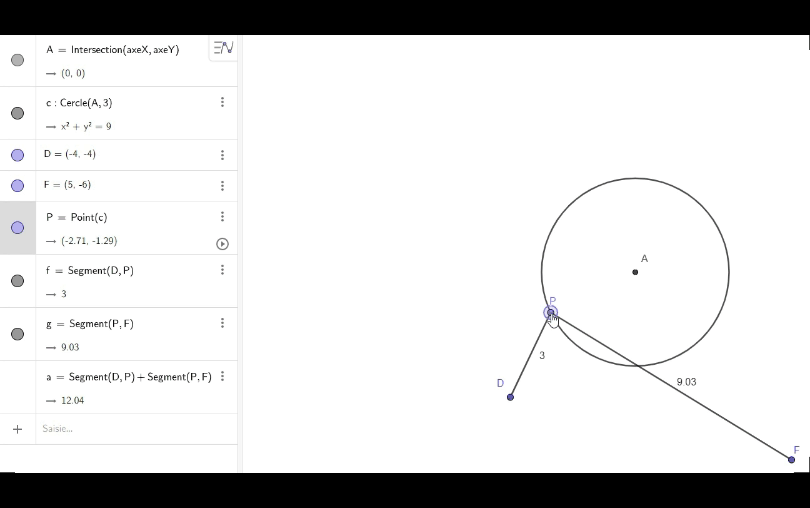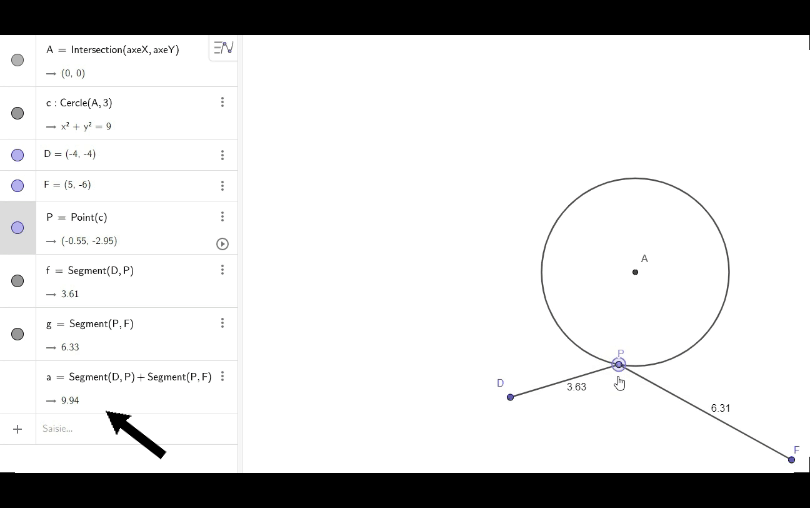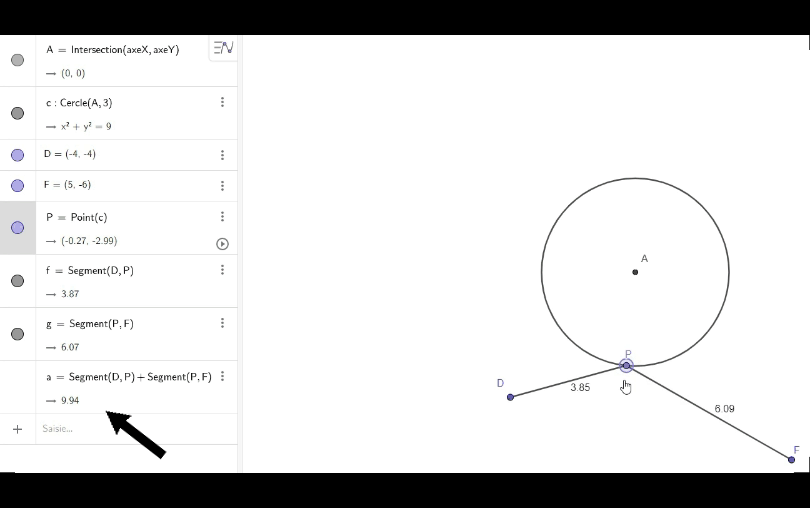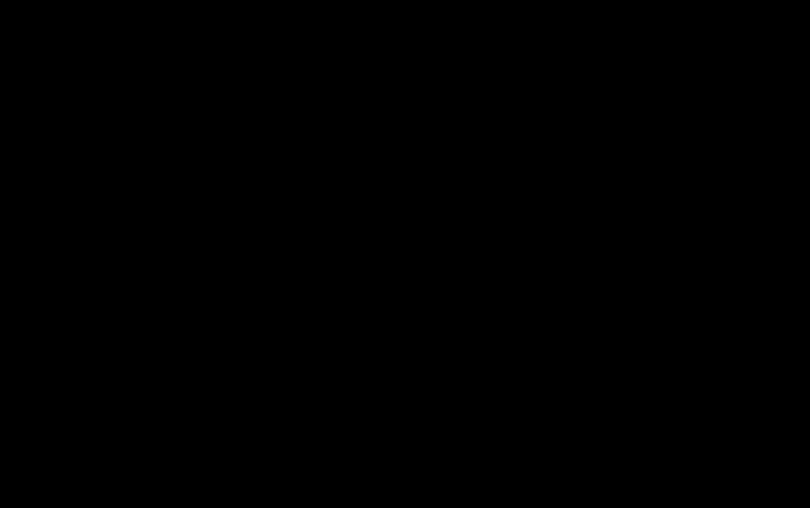
Ma première idée était de supposer que P était sur la bissectrice de l’angle \(\widehat{DAF}\), donc je m’empresse de tracer cette dernière:

Snif! Ce n’est pas ça…

J’ai donc réfléchir longtemps… longtemps… très longtemps… une vingtaine de minutes (quand-même!).

Conjecture

J’ai tracé les tangentes “sous-jacentes” au cercle passant par D et F, ai pris leur intersection I, puis ai tracé la droite (AI). Le point d’intersection de (AI) et du cercle semble passer par le point P trouvé précédemment.

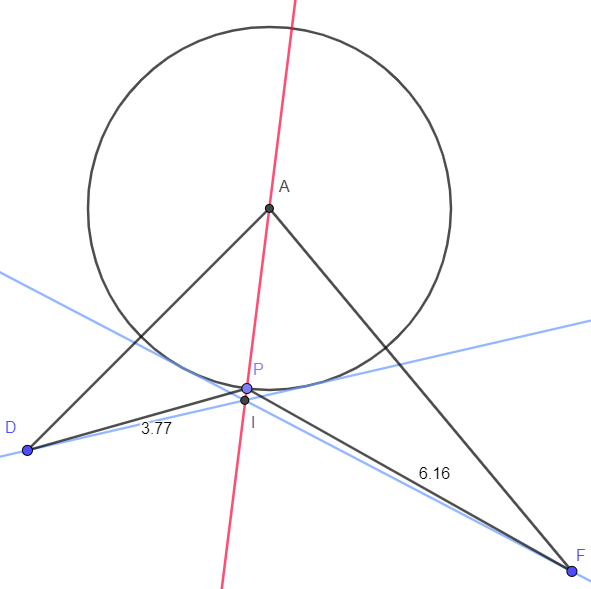
J’ai ensuite testé plusieurs autres configurations: cela semble exact ! Il ne reste plus qu’à le démontrer… mais là, je suis trop fatigué ! 🙂 Je reprendrai cet article quand j’aurai trouvé !

En attendant, vous pouvez faire mumuse avec le fichier geogebra :