Penchons-nous dans cet article sur l’évolution de la population mondiale et écoutons ce que Vérino dit sur cette évolution:
Évolution de la population mondiale: résumé en un tableau
| Années | Population mondiale (en milliards) |
|---|---|
| 1800 | 1 |
| 1927 | 2 |
| 1975 | 4 |
| 2022 | 8 |
Bien que les nombre de la deuxième colonne forment une suite géométrique de raison 2, on ne peut pas parler en ces termes car la différence entre chaque année n’est pas constante.
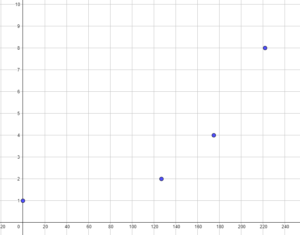
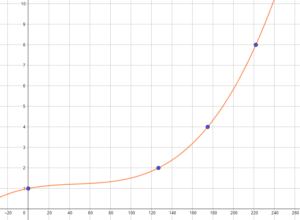
On peut toutefois entrevoir une évolution exponentielle à l’aide du graphique suivant:
Évolution de la population mondiale: interpolations
À ce stade, mathématiquement parlé, nous avons plusieurs possibilités d’interpolations: polynomiale ou exponentielle (on exclut direct l’interpolation affine vue la tronche de l’évolution…).
Évolution de la population mondiale: interpolation polynomiale
On pourrait penser que les quatre point du graphique précédent se trouvent (presque) sur une parabole… ou sur une courbe représentant un polynôme. Le but est donc de trouver une équation d’une fonction polynomiale passant par ces quatre points.
Interpolation quadratique
Dans un premier temps, on se penche sur une équation de degré 2… car franchement, les quatre points semblent former une belle parabole non ?
On cherche donc une fonction \(f\) telle que \(f(x)=ax^2+bx+1\) (« 1 » car la courbe passe par (0;1)).
Il nous faut donc exploiter deux des trois points restants.
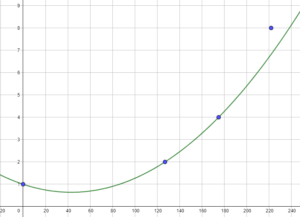
- En utilisant les points (127;2) et (175;4), on doit résoudre le système:$$\begin{cases}127^2a+127b+1=2\\175^2a+175b+1=4\end{cases}$$et on trouve alors:$$a=\frac{103}{533400},\quad b=-\frac{8881}{533400}.$$On obtient alors la courbe suivante:
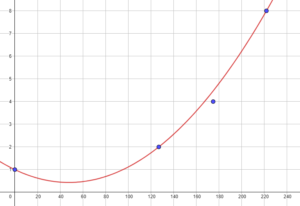
- En utilisant les points (127;2) et (222;8), on doit résoudre le système:$$\begin{cases}127^2a+127b+1=2,222^2a+222b+1=8\end{cases}$$et on trouve alors:$$a=\frac{667}{2678430},\quad b=-\frac{63619}{2678430}.$$On obtient alors la courbe suivante:
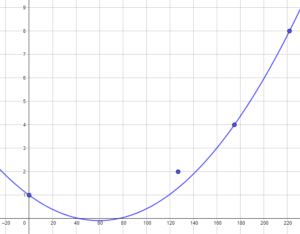
- En utilisant les points (175;4) et (222;8), on obtient:
Nous allons donc rejeter l’interpolation quadratique car… trop approximative et surtout… trop fausse! En effet, entre 1800 et 1927, il n’y a pas de baisse de la population mondiale donc ce genre d’approximation n’est pas cohérent.
Interpolation cubique: interpolation de Lagrange
On cherche un polynôme passant par TOUS les points. On va donc utiliser le polynôme d’interpolation de Lagrange: on cherche le polynôme P tel que
Le polynôme obtenu est alors:$$P(x)=\frac{20971 x^3}{17624069400}-\frac{976673 x^2}{5874689800}+\frac{86321677 x}{8812034700}+1.$$
Bien que passant par tous les points, cette interpolation n’est pas adaptée au contexte. En effet, pourquoi l’évolution suivrait-elle une progression polynomiale cubique ?
Sciences sans conscience n’est que ruine de l’âme.
Rabelais
Interpolation exponentielle
Nous le savons (sûrement), dès lors que nous parlons d’évolution naturelle, il est souvent question d’évolution exponentielle. Il est donc plus naturel de se pencher sur une extrapolation exponentielle.
Pour cela, nous allons prendre le logarithme népérien de la population:
| Années | Logarithme népérien de la population mondiale (en milliards) |
|---|---|
| 1800 | ln(1) = 0 |
| 1927 | ln(2) |
| 1975 | ln(4) |
| 2022 | ln(8) |
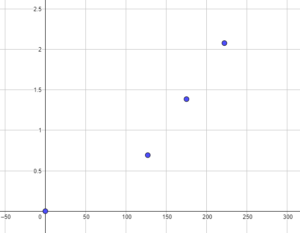
Et nous obtenons le graphique suivant:
Maintenant, nous allons faire une approximation affixe (un ajustement linéaire). On peut par exemple utiliser Python:
from numpy import polyfit, corrcoef # pour le calcul des coefficients de la droite de régression
from math import log
x = [ 0, 127, 175, 222 ]
y = [ 0, log(2), log(4), log(8) ] # consommations (L)
coef = polyfit( x , y , 1 )
a, b = round(coef[0],3) , round(coef[1],3)
r = round(corrcoef(x,y)[0][1],3)
print(f'a = {a}, b = {b}, r = {r}.')a = 0.009, b = -0.144, r = 0.965.
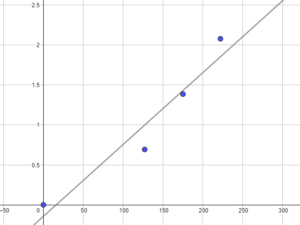
On peut ainsi dire que la droite d’équation \(y’ = 0,009x – 0,144\) est une approximation du logarithme népérien de la population mondiale.
Le coefficient de corrélation r n’est certes pas loin de 1, mais il aurait été mieux qu’il soit supérieur à 0,975 pour une corrélation mieux adaptée… Mais on va faire avec!
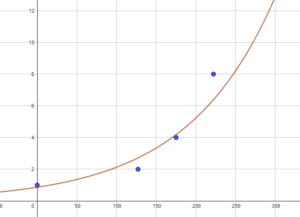
y‘ représente ln(y) donc:$$y = \text{e}^{0,009x – 0,144}.$$
Bien qu’au premier abord la courbe obtenue paraisse « loin » des points, c’est tout de même la meilleure approximation possible.
Avec cette approximation, en 2080, la population mondiale serait égale (en milliards) à:$$\text{e}^{0,009\times280 – 0,144}\approx=10,76.$$
Ainsi, je ne comprends pas comment les spécialistes ont prévu une population mondiale à 10,4 milliards en 2080… même si on n’est pas à 3 millions près à cette échelle…
La chaîne Youtube de Vérino: https://www.youtube.com/@Verinaze



Plutôt que de chercher une modélisation simpliste de la population mondiale globale, finalement comme un système régit par une équation différentielle linéaire du premier ordre, on pourrait la modéliser par zone géographique. Les prévisions démographiques sont très différentes d’un continent à l’autre. Par exemple, en Europe la pyramide des âges est déformée par le baby boom. En Afrique la mortalité infantile diminue. En Chine il existe une certaine planification d’état. De plus, l’effet régulateur de la limitation des ressources est différent selon les endroits : en Allemagne, certains couples ne font pas de deuxième enfant pour des raisons économiques alors qu’ils ont accès à davantage de ressources que des couples ailleurs dans le monde qui font plusieurs enfants. En conclusion, je pense que pour faire une bonne modélisation à horizon 2080, on pourrait prendre en compte, les pyramides des âges, l’espérance de vie et le taux de fécondité, dans les principaux pays du monde en termes de population.
Ce sujet est surtout un prétexte pour utiliser des outils de base. Je ne suis pas statisticien et n’aurai jamais la prétention de me substituer à l’un d’entre eux bien évidemment 🙂 Il y a en effet multitude de paramètres à prendre en compte, dont je n’ai pas la connaissance précise. Je ne suis que prof de lycée, rien de plus… 🙂