Dans ma vie professionnelle, et pas plus tard qu’hier, j’ai souvent eu à trouver l’équation d’une parabole passant par 3 points. Pourquoi ? Parce que dans les exercices que l’on propose aux élèves, c’est pratique!
Le problème est que le logiciel geobegra ne permet pas de le faire à ma connaissance.
Edit: un lecteur m’informe qu’il est facile de trouver une équation connaissant 3 points sous geogebra à l’aide de la fonction Polynome(A,B,C). En effet, cela fonctionne mais les coefficients sont des flottants. Ainsi, si l’on veut proposer une équation à des élèves, cela ne convient pas car les coefficients sont souvent des valeurs approchées.
J’ai donc dû m’y coller en Python…
Trouver l’équation d’une parabole passant par 3 points: aspect mathématique
Voyons avant tout l’aspect mathématique du problème. C’est assez simple: on connait les coordonnées de trois points, et on cherche les coefficients a, b et c de la fonction f(x) = ax² + bx + c de sorte que sa courbe représentative passe par les trois points.
Formallisation
On pose \(A(x_A;y_A)\), \(B(x_B;y_B)\) et \(C(x_C;y_C)\) nos trois points. On a alors le système:$$\left\{\begin{array}{l}ax_A^2+bx_A+c=y_A\\ax_B^2+bx_B+c=y_B\\ax_C^2+bx_C+c=y_C \end{array}\right.$$
Résolution algébrique
Ce système est un système linéaire de trois équations à trois inconnues, donc rien de bien méchant à résoudre…C’est juste un peu long si on le fait à la main. Mais nous n’allons pas le faire, bien sûr… car nous sommes des sacripants… 🙂
Nous allons écrire ce système de façon matricielle:$$\begin{pmatrix}x_A^2 & x_A & 1\\x_B^2 & x_B & 1\\x_C^2 & x_C & 1\\ \end{pmatrix}\begin{pmatrix}a\\b\\c\end{pmatrix}=\begin{pmatrix}y_A\\y_B\\y_C\end{pmatrix}.$$
On en déduit alors:$$\begin{pmatrix}a\\b\\c\end{pmatrix}=\begin{pmatrix}y_A\\y_B\\y_C\end{pmatrix}\begin{pmatrix}x_A^2 & x_A & 1\\x_B^2 & x_B & 1\\x_C^2 & x_C & 1\\ \end{pmatrix}^{-1}.$$
Trouver l’équation d’une parabole passant par 3 points: implémentation en Python
Il existe une méthode pour résoudre de tels systèmes linéaires en Python. Avec le module numpy et linalg.solve, l’affaire est pliée… Sauf que la plupart du temps, le système est résolu sur les flottants et donne donc comme résultats des nombres en valeurs approchées! Scrogneugneu! C’est carrément naze! Il nous faut donc mettre ce qui nous sert de cerveau en mode cogitum.
Des coefficients rationnels
L’idée est de manipuler des rationnels, et non des flottants. On ne va donc pas utiliser numpy mais sympy qui, d’ailleurs, est quand-même approprié pour faire de l’algèbre.
from sympy import Matrix, Rational
def parabola(A,B,C):
L = [A,B,C]
matrice = Matrix([[Rational(a**2),Rational(a),Rational(1)] for a,b in L])
other = Matrix([[Rational(b)] for a,b in L])
return matrice.solve(other)
if __name__ == '__main__':
A, B, C = (-5,4), (0,-3), (7,5)
P = parabola(A,B,C)Voilà! Avec la fonction parabola, j’ai la matrice des coefficients a, b, c. Il nous faut maintenant peaufiner tout ça.
Tracé de la parabole en Python
Une fois l’expression de la parabole obtenue, je vais la tracer. Je vais définir alors les deux fonctions suivantes.
from sympy import Matrix, Rational, latex
import matplotlib.pyplot as plt
import numpy as np
def f(P,x):
return P[0]*x*x + P[1]*x + P[2]
def draw_parabola(A, B, C):
P = parabola(A,B,C)
x = np.linspace(-10, 10, 400)
y = f(P,x)
# Convertir les coefficients en chaînes de caractères LaTeX
P_latex = [latex(P[i]) for i in range(3)]
chaine = rf'$f(x) = {P_latex[0]}x^2'
if P[1] < 0:
chaine += rf' {P_latex[1]}x'
else:
chaine += rf' + {P_latex[1]}x'
if P[2] < 0:
chaine += rf' {P_latex[2]}$'
else:
chaine += rf' + {P_latex[2]}$'
plt.plot(x, y, label=chaine)
# Ajouter les points
for a,b in [A,B,C]:
plt.scatter(a, b, color='red', zorder=5)
plt.annotate(f'({a},{b})', (a, b), textcoords="offset points", xytext=(-15,-10), ha='center', color='red')
plt.title('Graphique de la fonction f(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
# Afficher la grille
plt.grid(True)
# Afficher le graphique
plt.show()Là, une magnifique courbe se dessine alors, faisant apparaître les trois points imposés.
Tracé de la courbe en \(LaTeX\)
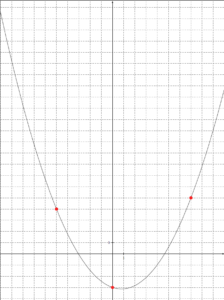
Si on souhaite créer de beaux devoirs pour nos chers chérubins, le graphique à la matplotlib ne suffira pas nécessairement. Le top du top, c’est tout de même d’avoir un graphique en \(\LaTeX\). Alors soit!
On va créer une fonction qui crée la courbe en \(\LaTeX\) à l’aide de TiKZ.
import os
def export_latex(A, B, C, x_range=(-10, 10), num_points=100):
P = parabola(A,B,C)
# Convertir les coefficients en chaînes de caractères LaTeX
P_latex = [ '({}/{})'.format(P[i].numerator,P[i].denominator) for i in range(3)]
y_min, y_max = 0,0
x = x_range[0]
while x <= x_range[1]:
if P[0]*x*x+P[1]*x+P[2] < y_min:
y_min = P[0]*x*x+P[1]*x+P[2]
if P[0]*x*x+P[1]*x+P[2] > y_max:
y_max = P[0]*x*x+P[1]*x+P[2]
x += (x_range[1]-x_range[0])/num_points
y_min, y_max = y_min-1, y_max+1
points_latex = ''
for x,y in [A,B,C]:
points_latex += f"""
\\fill[red] ({x},{y}) circle (4pt);\n
"""
tikz_code = f"""
\\documentclass{{standalone}}
\\usepackage{{tikz}}
\\begin{{document}}
\\begin{{tikzpicture}}
\\draw[gray,dashed] ({x_range[0]},{y_min}) grid ({x_range[1]},{y_max});
\\draw[thick,->,>=latex] ({x_range[0]},0) -- ({x_range[1]},0);
\\draw[thick,->,>=latex] (0,{y_min}) -- (0,{y_max});
\\draw[thick] (1,0.1) -- (1,-0.1) node[below] {{1}};
\\draw[thick] (0.1,1) -- (-0.1,1) node[left] {{1}};
\\draw[thick, smooth, domain={x_range[0]}:{x_range[1]}, samples={num_points}] plot (\\x, {{ {P_latex[0]}*\\x*\\x + {P_latex[1]}*\\x + {P_latex[2]} }});
{points_latex}
\\end{{tikzpicture}}
\\end{{document}}
"""
with open('parabola_plot.tex', 'w') as f:
f.write(tikz_code)
cmd = "pdflatex --shell-escape -synctex=1 -interaction=nonstopmode parabola_plot.tex"
os.system(cmd)
readpdf = "START parabola_plot.pdf"
os.system(readpdf)Voili-voilou!
Cette fonction exporte le fichier \(\LaTeX\), puis le compile via PdfLaTeX. Ainsi, on peut le retoucher si besoin est.
Il y a fort à parier que ce code est à conserver dans vos outils de profs, n’est-ce pas ? ça vous laissera plus de temps pour regarder Netflix 🙂 (bon, là, je parle pour moi…).
Le script complet
# -*- coding: utf-8 -*-
"""
Created on Fri May 17 18:13:53 2024
@author: Stéphane Pasquet
@url: https://www.mathweb.fr/euclide/2024/05/18/trouver-lequation-dune-parabole-passant-par-3-points/
"""
from sympy import Matrix, Rational, latex
import matplotlib.pyplot as plt
import numpy as np
import os
# retourne a, b, x de y = ax² + bx + c, où A, B, C sont sur la parabole
def parabola(A,B,C):
L = [A,B,C]
matrice = Matrix([[Rational(a**2),Rational(a),Rational(1)] for a,b in L])
other = Matrix([[Rational(b)] for a,b in L])
return matrice.solve(other)
def f(P,x):
return P[0]*x*x + P[1]*x + P[2]
def draw_parabola(A, B, C):
P = parabola(A,B,C)
x = np.linspace(-10, 10, 400)
y = f(P,x)
# Convertir les coefficients en chaînes de caractères LaTeX
P_latex = [latex(P[i]) for i in range(3)]
chaine = rf'$f(x) = {P_latex[0]}x^2'
if P[1] < 0:
chaine += rf' {P_latex[1]}x'
else:
chaine += rf' + {P_latex[1]}x'
if P[2] < 0:
chaine += rf' {P_latex[2]}$'
else:
chaine += rf' + {P_latex[2]}$'
plt.plot(x, y, label=chaine)
# Ajouter les points
for a,b in [A,B,C]:
plt.scatter(a, b, color='red', zorder=5)
plt.annotate(f'({a},{b})', (a, b), textcoords="offset points", xytext=(-15,-10), ha='center', color='red')
plt.title('Graphique de la fonction f(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
# Afficher la grille
plt.grid(True)
# Afficher le graphique
plt.show()
def export_latex(A, B, C, x_range=(-10, 10), num_points=100):
P = parabola(A,B,C)
# Convertir les coefficients en chaînes de caractères LaTeX
P_latex = [ '({}/{})'.format(P[i].numerator,P[i].denominator) for i in range(3)]
y_min, y_max = 0,0
x = x_range[0]
while x <= x_range[1]:
if P[0]*x*x+P[1]*x+P[2] < y_min:
y_min = P[0]*x*x+P[1]*x+P[2]
if P[0]*x*x+P[1]*x+P[2] > y_max:
y_max = P[0]*x*x+P[1]*x+P[2]
x += (x_range[1]-x_range[0])/num_points
y_min, y_max = y_min-1, y_max+1
points_latex = ''
for x,y in [A,B,C]:
points_latex += f"""
\\fill[red] ({x},{y}) circle (4pt);\n
"""
tikz_code = f"""
\\documentclass{{standalone}}
\\usepackage{{tikz}}
\\begin{{document}}
\\begin{{tikzpicture}}
\\draw[gray,dashed] ({x_range[0]},{y_min}) grid ({x_range[1]},{y_max});
\\draw[thick,->,>=latex] ({x_range[0]},0) -- ({x_range[1]},0);
\\draw[thick,->,>=latex] (0,{y_min}) -- (0,{y_max});
\\draw[thick] (1,0.1) -- (1,-0.1) node[below] {{1}};
\\draw[thick] (0.1,1) -- (-0.1,1) node[left] {{1}};
\\draw[thick, smooth, domain={x_range[0]}:{x_range[1]}, samples={num_points}] plot (\\x, {{ {P_latex[0]}*\\x*\\x + {P_latex[1]}*\\x + {P_latex[2]} }});
{points_latex}
\\end{{tikzpicture}}
\\end{{document}}
"""
with open('parabola_plot.tex', 'w') as f:
f.write(tikz_code)
cmd = "pdflatex --shell-escape -synctex=1 -interaction=nonstopmode parabola_plot.tex"
os.system(cmd)
readpdf = "START parabola_plot.pdf"
os.system(readpdf)
if __name__ == '__main__':
A, B, C = (-5,4), (0,-3), (7,5)
draw_parabola(A, B, C)
export_latex(A, B, C)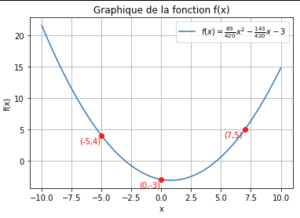



Bonjour,
Dans geogebra, Polynôme(A, B, C), trace la parabole passant par A, B et C. C’est très utile pour les activités de modélisation polynomiale avec les élèves.
En python, c’est toujours intéressant.
Cdt
Vincek
Ah! Ce n’est pas faute d’avoir cherché, mais avec Geogebra, c’est pas évident de trouver ce que l’on cherche des fois… Il y a tellement de fonctionnalités. Merci beaucoup. Cependant, Geogebra ne donne que des coefficients flottants… Et c’est ce que je ne veux pas 🙂