La méthode de la sécante, que nous allons implémenter en Python, est une méthode algorithmique de résolution d’équation.
Elle est fortement inspirée de la méthode de Newton.
Principe mathématique de la méthode de la sécante (avant implémentation en Python)
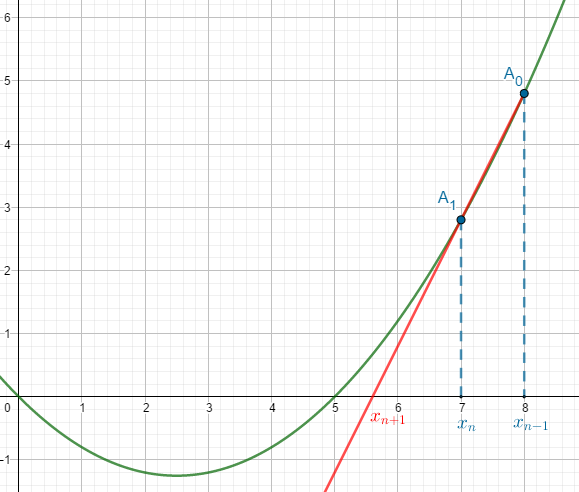
Nous avons pu voir à travers la méthode de Newton que la suite définie par:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ convergeait vers la solution de l’équation f(x) = 0.
Le principal inconvénient de cette méthode est le fait que l’on ne connait pas nécessairement la dérivée de la fonction f. Aussi, nous allons remplacer \(f'(x_n)\) par \(\displaystyle\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}\), qui est une bonne approximation pour \(x_n\) et \(x_{n-1}\) très proches.
La relation de récurrence devient donc:$$x_{n+1}=x_n-\frac{(x_n-x_{n-1})f(x_n)}{f(x_n)-f(x_{n-1})}.$$
Implémentation en Python
def secante(a,b,p):
while True:
x = b - ( b - a ) * f(b) / ( f(b) - f(a) )
if abs(x - b) <= 10**(-p):
return x
else:
a, b = b, xIl n’y a rien de bien compliqué ici: la fonction admet 3 arguments (a et b représentent respectivement le premier et le deuxième terme de la suite, et p la précision souhaitée).
On calcule ensuite le terme suivant (→ ligne 3) et on regarde la différence entre cette dernière valeur et celle du terme précédent. Si elle est inférieure à \(10^{-p}\), on retourne la dernière valeur calculée (et la boucle s’arrête), sinon a et b deviennent b et x.
En d’autres termes, a représente \(x_{n-1}\), b représente \(x_n\) et x représente \(x_{n+1}\).
Bien entendu, il ne faut pas oublier de définir la fonction f. Par exemple, pour \(f(x)=0,2(x-10)^2+3x-20\):
def f(x):
return 0.2 * (x-10)**2 + 3*x - 20
>>> secante(8,7,10) 5.000000000000002
La valeur exacte de la solution la plus proche de 7 étant 5, on obtient un assez bon résultat.
N’oubliez pas que si vous avez des difficultés en mathématiques, je peux vous aider par webcam !