La méthode des rectangles est une méthode algorithmique permettant d’encadrer l’aire d’un domaine sous une courbe représentative de fonction et sur un intervalle donné.
Principe mathématique de la méthode des rectangles
Considérons une fonction f continue sur un intervalle [a ; b], et subdivisons cet intervalle en n, c’est-à-dire coupons-le en n petits intervalles de même amplitude. Ces subdivisions seront les “bases” de rectangles.
Notons:$$x_k = a + \frac{b-a}{n}k$$ pour \(k\) entier compris entre 0 et n inclus, et considérons les rectangles:
- \(I_k\), de base \([x_k;x_{k+1}]\) et de hauteur \(f(x_k)\) pour \(0 \leqslant k \leqslant n-1\);
- \(J_k\), de base \([x_k;x_{k+1}]\) et de hauteur \(f(x_{k+1})\) pour \( 0\leqslant k \leqslant n-1\).
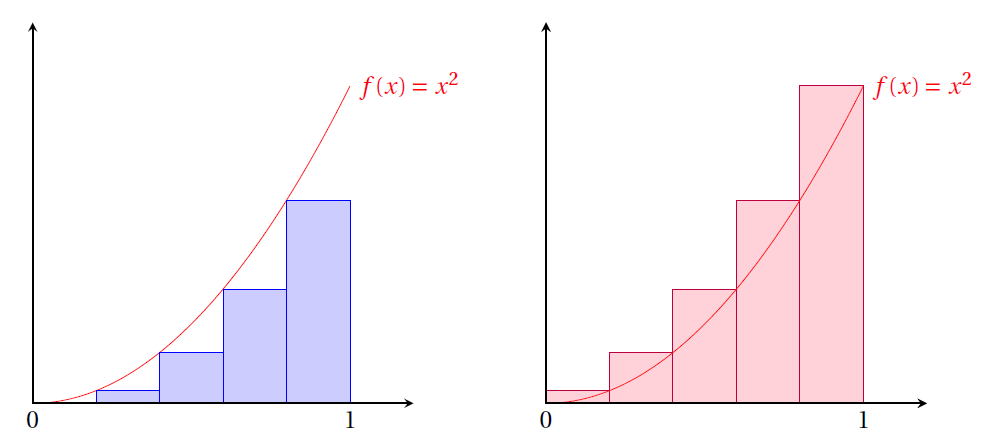
À droite : les rectangles \(J_k\) sur [0;1] subdivisé en n = 5
Intuitivement, plus le nombre de rectangles grandit, plus les sommes des aires des rectangles vont se rapprocher vers l’intégrale de la fonction sur le même intervalle.
Autrement écrit, si \(\mathcal{A}_n(I)\) et \(\mathcal{A}_n(J)\) représentent respectivement la somme des aires des rectangles I et J, alors:$$\lim\limits_{n\to+\infty}\mathcal{A}_n(I) = \lim\limits_{n\to+\infty}\mathcal{A}_n(J) = \int_a^b f(x)\text{d}x.$$De plus, si f est strictement croissante sur [a ; b]:$$\mathcal{A}_n(I) \leqslant \int_a^b f(x)\text{d}x \leqslant \mathcal{A}_n(J).$$Si la fonction est strictement décroissante, l’encadrement est bien entendu inversé.
Ainsi, si on arrive à calculer \(\mathcal{A}_n(I)\) et \(\mathcal{A}_n(J)\), on aura un encadrement de l’intégrale.
Implémentation en Python
def integrale(f,a,b,n):
longueur = (b - a) / n
aire_inf , aire_sup = 0 , 0
for k in range (n):
aire_inf = aire_inf + longueur * f(a + k * longueur )
aire_sup = aire_sup + longueur * f(a + (k+1) * longueur )
return aire_inf , aire_sup
aire_inf , aire_sup = integrale( lambda x: x*x , 0 , 1 , 100 )
print("{} < integrale < {}".format(aire_inf,aire_sup))
Il n’y a rien de bien compliqué du point de vue algorithmique; en effet,
- on commence par définir l’amplitude des subdivisions → ligne 2
- ensuite, on initialise les deux aires à calculer à 0 → ligne 3
- puis on fait une boucle en k (pour k variant de 0 à n-1 → ligne 4) dans laquelle on ajoute aux variables représentant les deux aires l’aire du rectangle \(I_k\) et celle du rectangle \(J_k\) (→lignes 5 et 6)
- À la fin de la boucle, on retourne les valeurs stockées dans les variables représentant les deux aires (→ ligne 7)
Il est à noter la syntaxe particulière de la fonction en Python: j’utilise ici l’opérateur lambda, qui me semble très pratique. Cela étant dit, on peut aussi utiliser une autre syntaxe peut-être plus naturelle:
def integrale(a,b,n):
longueur = (b - a) / n
aire_inf , aire_sup = 0 , 0
for k in range (n):
aire_inf = aire_inf + longueur * f(a + k * longueur )
aire_sup = aire_sup + longueur * f(a + (k+1) * longueur )
return aire_inf , aire_sup
def f(x):
return x**2
aire_inf , aire_sup = integrale( 0 , 1 , 100 )
print("{} < integrale < {}".format(aire_inf,aire_sup))
Dans ce dernier script, la fonction est définie à part. On enlève donc l’argument représentant la fonction f de la fonction Python integrale.
Pour information, en lançant ce script, s’affiche le résultat suivant:
0.32835000000000014 < integrale < 0.33835000000000015
Et en augmentant considérablement la valeur de n à 1000000, on arrive (mais à quel coût !) à:
0.3333328333334962 < integrale < 0.3333338333334962
Sachant que la valeur exacte est \(\frac{1}{3}\), cette méthode ne semble pas réellement efficace. En effet, pour \(n=10^6\), nous n’avons qu’une valeur approchée à \(10^{-6}\), ce qui laisse à penser que la complexité de cette méthode est linéaire, ce qui peut poser problème pour de très grandes valeurs de n. D’ailleurs, lancez le script et voyez le temps que cela prend pour \(n=10^{12}\)… Spoiler alert: soyez très patient·e·s !
Il existe d’autres méthodes permettant d’obtenir une valeur approchée d’une intégrale. Je vous en présente une sur cette page, tout aussi lente. Il en existe tout de même des plus rapides comme celle utilisée par certaines calculatrices : la méthode de Simpson.
Complément: dessiner les rectangles
Voici un script qui permet de dessiner les rectangles inférieurs et supérieurs:
import numpy as np
import matplotlib.pyplot as plt
def rectangle(n, f, a, b, label=None):
"""
Trace f(x) sur [a,b] et affiche les rectangles gauche (inf.) et droite (sup.)
Si label est None, affiche 'f(x)' comme label.
Retourne (aire_left, aire_right).
"""
if n < 1 or not isinstance(n, int):
raise ValueError("n doit être un entier >= 1")
dx = (b - a) / n
left_edges = np.linspace(a, b - dx, n)
right_edges = np.linspace(a + dx, b, n)
heights_left = f(left_edges)
heights_right = f(right_edges)
area_left = np.sum(heights_left * dx)
area_right = np.sum(heights_right * dx)
is_increasing = f(b) >= f(a)
x_plot = np.linspace(a, b, 400)
plt.figure(figsize=(8, 5))
plt.plot(x_plot, f(x_plot), 'k', label=label or "f(x)", linewidth=2)
if is_increasing:
# Trace orange d'abord (en dessous), puis bleu (dessus)
plt.bar(right_edges - dx, heights_right, width=dx, align='edge',
edgecolor='black', alpha=0.35, color='orange',
label=f"Sup., Aire={area_right:.6f}")
plt.bar(left_edges, heights_left, width=dx, align='edge',
edgecolor='black', alpha=0.35, color='blue',
label=f"Inf., Aire={area_left:.6f}")
else:
# Trace bleu d'abord, puis orange (ordre original)
plt.bar(left_edges, heights_left, width=dx, align='edge',
edgecolor='black', alpha=0.35, color='blue',
label=f"Inf., Aire={area_left:.6f}")
plt.bar(right_edges - dx, heights_right, width=dx, align='edge',
edgecolor='black', alpha=0.35, color='orange',
label=f"Sup., Aire={area_right:.6f}")
ymin = min(0, float(np.min(heights_left)), float(np.min(heights_right)))
ymax = max(float(np.max(heights_left)), float(np.max(heights_right)))
plt.xlim(a - 0.02 * (b - a), b + 0.02 * (b - a))
plt.ylim(ymin - 0.05 * (ymax - ymin + 1e-9), ymax + 0.05 * (ymax - ymin + 1e-9))
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title(f"Méthodes des rectangles (n={n})")
plt.legend()
plt.grid(alpha=0.2)
plt.show()
return area_left, area_right
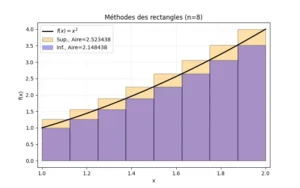
rectangle(8, lambda x: x**2, 1, 2, label=r"$f(x)=x^2$" ) # f(x)=x^2 --> l'affichage de ce script sur ce site présente l'expression sous la forme LaTeX mais c'est ainsi que l'on doit l'écrire
Et n’oubliez pas que si vous avez des difficultés en mathématiques, je peux vous aider par wecam !
je crois que y’a une erreur c’est si lim(A_n(I)) (n–>+inf) = lim (A_n(S)) = intégrale de a à b de f(x) pas A_n(J)
En effet, il y a eu une confusion entre S et J… Ces deux lettres représentant la même chose au final. J’ai rectifié cela en remplaçant tous les S par des J. Merci !