Nous allons voir comment créer un nuage de points représentant une suite numérique (arithmétique, géométrique ou autre) avec Python.

Le principe est très simple: utiliser matplotlib, une librairie de Python, pour construire le nuage de points associés à n’importe quelle suite numérique.

Nuage de points d’une suite arithmétique avec Python

Prenons l’exemple de la suite \( (u_n) \) définie pour tout entier naturel \(n\) par:$$\begin{cases}u_0=-3\\u_{n+1}=u_n+2,5\end{cases}$$

import matplotlib.pyplot as plt

def u(n):
    if n == 0:
        return -3 # valeur de u(0)
    
    return u(n-1) + 2.5

x = [ n for n in range(10) ] 
y = [ u(n) for n in range(10) ]

plt.scatter(x,y)

plt.title('Nuage de points : suite arithmétique')
plt.xlabel('x')
plt.ylabel('y')

plt.show()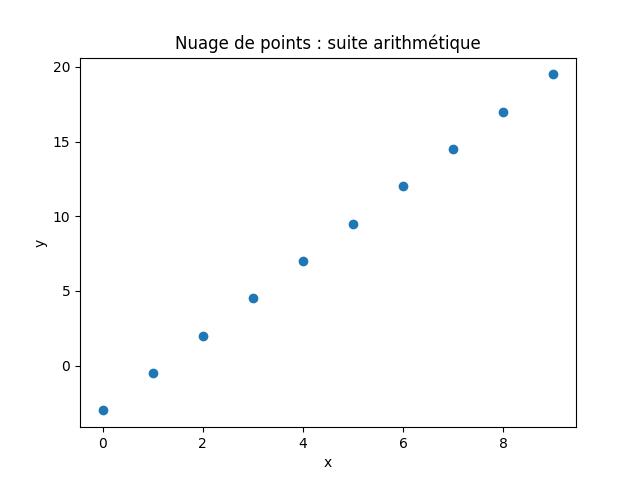

L’idée est de construire deux listes:

• une liste « x » contenant toutes les valeurs de l’indice n (ligne 9);
• une liste « y » contenant toutes les valeurs de \(u_n\) pour n variant dans la liste « x ».

Remarquez que nous avons construit les listes par compréhension, ce qui va plus vite. Sinon, à la place des lignes 9 et 10, on aurait pu écrire:

x , y = [] , []
for n in range(10):
    x.append(n)
    y.append( u(n) )

Pour notre exemple, les listes « x » et « y » donnent alors:

x = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
y = [-3, -0.5, 2.0, 4.5, 7.0, 9.5, 12.0, 14.5, 17.0, 19.5]

Ensuite, on demande à la fonction scatter de mettre tous les points de coordonnées \( (x_i;y_i) \).

Bien entendu, je me suis ici limité à 10 termes, mais on peut moduler ce nombre en changeant le paramètre de la fonction range aux lignes 9 et 10.

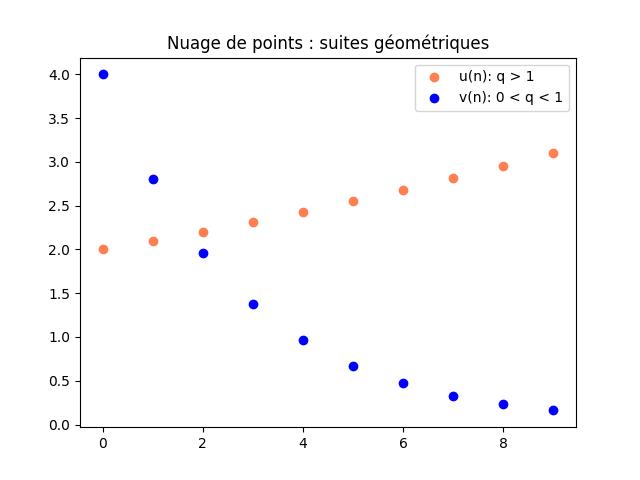
Nuage de points d’une suite géométrique avec Python

Prenons l’exemple des suites \( (u_n) \) et \( (v_n) \) définies pour tout entier naturel \(n\) par:$$\begin{cases}u_0=2\\u_{n+1}=1,05u_n\end{cases}\quad\text{et}\quad\begin{cases}v_0=4\\v_{n+1}=0,7v_n\end{cases}$$

import matplotlib.pyplot as plt

def u(n):
    if n == 0:
        return 2 # valeur de u(0)
    
    return u(n-1) * 1.05

def v(n):
    if n == 0:
        return 4 # valeur de v(0)
    
    return v(n-1) * 0.7

x = [ n for n in range(10) ] 
y = [ u(n) for n in range(10) ]
z = [ v(n) for n in range(10) ]

plt.scatter(x , y , c = 'coral' , label = 'u(n): q > 1')
plt.scatter(x , z , c = 'blue' , label = 'v(n): 0 < q < 1')

plt.title('Nuage de points : suites géométriques')
plt.legend()
plt.savefig('nuage-points-suites-geometriques-python.jpg')
plt.show()

Afin de construire plusieurs nuages de points, il suffit de faire appel à scatter autant de fois qu’il y a de nuages à construire. Pour les différencier, il faudra alors utiliser des couleurs.

La liste des couleurs est disponible sur la page https://matplotlib.org/stable/gallery/color/named_colors.html.

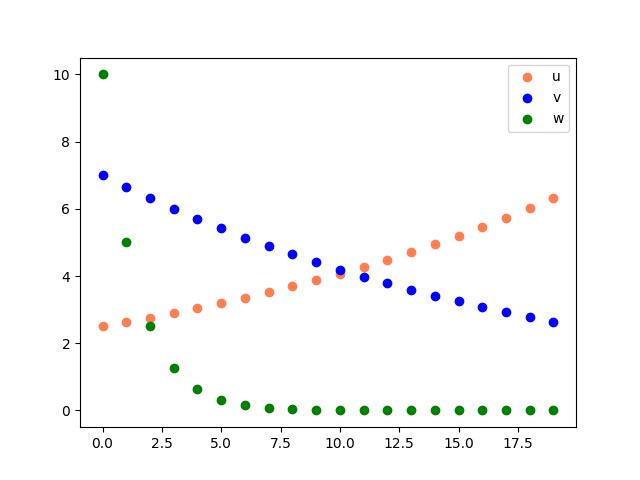
Nuages de points d’une suite quelconque avec Python

Pour simplifier les choses, on pourrait imaginer une fonction trace qui tracerait toutes les suites d’un seul coup. Je vous propose alors le programme suivant:

import matplotlib.pyplot as plt

def trace(n , suites_liste , couleurs_liste , labels_liste , titre , save = False, name = 'nuage.jpg'):
    x = [ k for k in range(n) ]
    for suite in suites_liste:
        i = suites_liste.index(suite)
        y = [ suite(k) for k in range(n) ]
        plt.scatter(x , y , c = couleurs_liste[i] , label = labels_liste[i])
    
    plt.legend()
    if save == True:
        plt.savefig(name)
    plt.show()

Ici, la difficulté est d’informer l’expression de chacune des suites. J’ai opté pour la syntaxe lambda. Par exemple,

u = lambda k: 1.05*u(k-1) if k>=1 else 2.5

désignera la suite géométrique de premier terme 2,5 et de raison 1,05.

Cela donne par exemple:

u = lambda k: 1.05*u(k-1) if k>=1 else 2.5
v = lambda k: 0.95*v(k-1) if k>=1 else 7
w = lambda k: 0.5*w(k-1) if k>=1 else 10

L = [u,v,w]
C = ['coral','blue','green']
LAB = ['u','v','w']
titre = 'Nuage de points : suites géométriques'

trace(20,L,C,LAB,'Nuage de points : suites géométriques',titre)