Un problème mathématique d’aire
Il y a quelques temps, j’ai vu le problème mathématique d’aire suivant: étant donnée la figure suivante, trouver l’aire manquante.
Trouver la distance entre deux centres de cercles
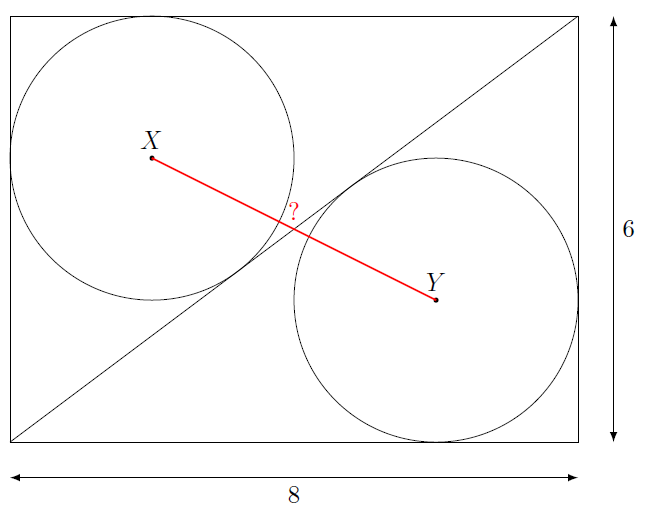
Comment trouver la distance entre les centres des deux cercles ci-dessous ? ici, ces cercles sont tangents à la diagonale tracée ainsi qu’aux côtés du rectangle.
Trouver l’aire d’un triangle dans une figure donnée
Nous allons aujourd’hui regarder comment déterminer l’aire du triangle bleu de la figure ci-dessous, de deux manières différentes.
(suite…)Trouver une aire
Comment exprimer en fonction de x, y et z l’aire w ?
Ce problème peut être abordé comme application dans le chapitre des polynômes de degré 2…
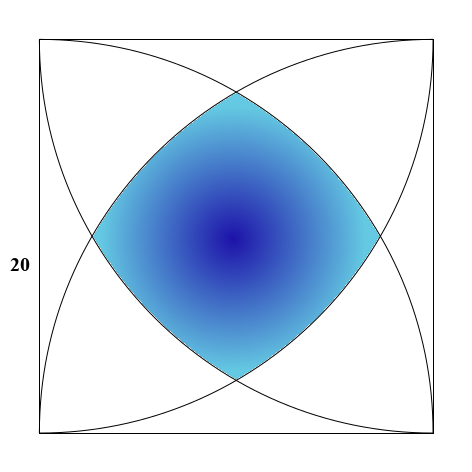
(suite…)Trouver une aire
Le problème est le suivant : trouver l’aire du domaine représenté en bleu sur la figure ci-dessous:
Pourquoi l’aire d’un disque est égale à \(\pi r^2\) ?
Considérons un disque de rayon r. Nous allons rapporté le plan à un repère orthonormé d’origine O, et nous allons centrer notre disque en O.
Aire entre trois cercles tangents
Cet article a pour objectifs de construire trois cercles tangents de rayons différents et de calculer l’aire du domaine compris entre ces trois cercles.
(suite…)Le théorème de Pick
On considère un polygone convexe, c’est-à-dire une figure géométrique constituée de plusieurs côtés rectilignes de sorte qu’aucun sommet ne « rentre » dans la figure, sur un maillage régulier de sorte que chaque sommet soit sur un nœud de ce maillage comme l’illustre le schéma ci-dessous.
Le théorème de Pick stipule que la superficie du polygone peut être calculée de façon simple à l’aide de la formule : \[ \mathcal{A}=i+\frac{b}{2}-1\]
exprimée en unités d’aire, où « i » représente le nombre de nœuds intérieurs au polygone et « b » celui des nœuds se trouvant sur ses côtés.