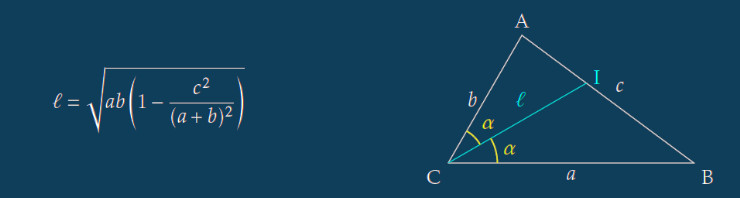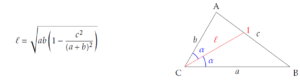Comment mélanger le calcul littéral, la géométrie (dans un cercle) et mettre le tout dans une démonstration? Oui, je sais que le résultat auquel nous allons aboutir n’est plus au programme du collège, mais cela n’empêche pas de se pencher sur sa démonstration, qui fait intervenir le calcul littéral (qui est encore au programme… profitons-en!).
Nous allons voir dans cet article une preuve (bien entendu erronée) que 2 = 4. Ce que nous allons voir est compréhensible par des élèves de Terminale ayant vu la notion de continuité de fonctions.
(suite…)On considère un polynôme à coefficients entiers : $$P(X)=\sum_{k=0}^n c_kX^k\quad,\quad \forall\; k\in[0;n]\cap\mathbb{N},\ c_k\in\mathbb{Z}.$$L’objectif ici est de démontrer que s’il admet une racine rationnelle irréductible \(\frac{a}{b}\) alors \(a\) divise \(c_0\) et \(b\) divise \(c_ n\).
(suite…)Giulio Fagnano était un mathématicien italien de la fin du XVIIe siècle.
Il a probablement été le premier à s’être intéressé à la théorie des intégrales elliptiques, mais ce n’est pas l’objet de cet article.
Le problème connu sous le nom de problème de Fagnano est le suivant :
(suite…)Peut-on inscrire un triangle de périmètre minimal dans un triangle acutangle ?
On considère un polygone convexe, c’est-à-dire une figure géométrique constituée de plusieurs côtés rectilignes de sorte qu’aucun sommet ne “rentre” dans la figure, sur un maillage régulier de sorte que chaque sommet soit sur un nœud de ce maillage comme l’illustre le schéma ci-dessous.
Le théorème de Pick stipule que la superficie du polygone peut être calculée de façon simple à l’aide de la formule : \[ \mathcal{A}=i+\frac{b}{2}-1\]
exprimée en unités d’aire, où “i” représente le nombre de nœuds intérieurs au polygone et “b” celui des nœuds se trouvant sur ses côtés.
Le théorème de Viviani stipule que : “dans un triangle équilatéral, la somme des distances d’un point intérieur quelconque aux trois côtés est constante.”
Autrement dit, quelle que soit la position du point M dans le triangle ABC, \[ \text{MS}+\text{MQ}+\text{MO} = \text{constante}.\]
(suite…)
Longueur d’une bissectrice dans un triangle: considérons un triangle quelconque ABC ; posons alors AB = c, AC = b et BC = a.
Posons \(\ell\) la longueur de la bissectrice issue de C ; alors, on a:
Démontrons ce résultat…
(suite…)À l’école primaire, les élèves prennent connaissance de l’existence d’un nombre mystérieux nommé “Pi” et noté par la lettre grecque “\(\pi\)” par Archimède, en rapport avec l’initiale du mot “\(\pi\varepsilon\rho\iota\mu\varepsilon\tau\rho o\zeta\)” (“périmètre” en français).
À ce stade de l’apprentissage, les professeurs des écoles disent que la valeur de Pi est 3,14 et j’espère qu’ils ajoutent que ce n’est qu’une valeur approchée de ce nombre qui admet une partie décimale infinie. D’ailleurs, tout nombre qui ne peut pas s’écrire entièrement est désigné par une lettre ou autre chose de “rapide à écrire” et c’est la raison pour laquelle Pi est désigné par une lettre : on ne peut pas l’écrire en entier.
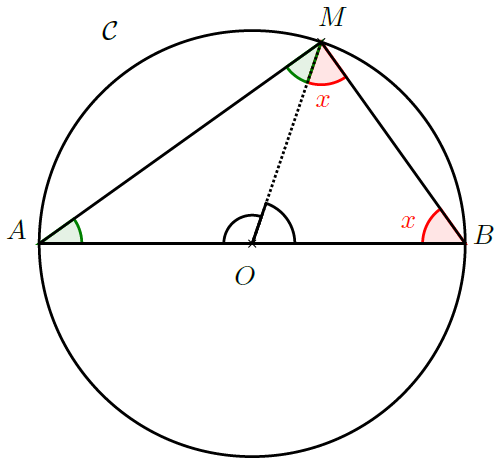
On définit le nombre \(\pi\) comme étant le rapport constant entre le périmètre d’un cercle et son diamètre (il faut entendre ici : dans le plan euclidien). Mais pourquoi ce rapport est-il constant ? Comment a-t-on pu démontrer que \(\pi\) existait ? Nous allons le voir ici …
(suite…)Absurdité mathématique : ça, c’est fun ! Il y a forcément une erreur, mais où ? C’est un jeu amusant auquel on peut participer pour améliorer notre réflexion. C’est comme les paradoxes mathématiques !
(suite…)