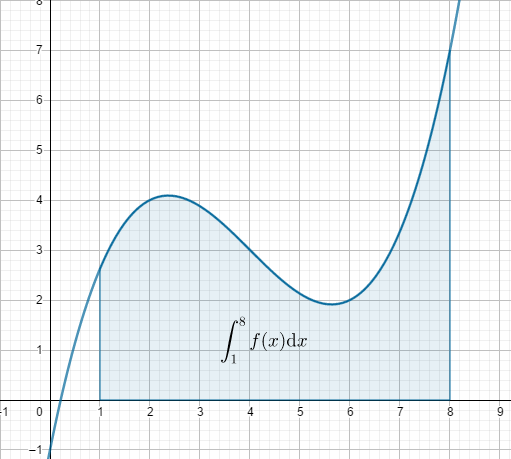
La méthode des rectangles (cliquez pour voir une vidéo explicative), aussi expliquée sur ce site ici) est une méthode algorithmique (que l’on peut implémenter en Python par exemple) qui permet d’obtenir un encadrement d’une intégrale. Je rappelle que pour une fonction positive sur un intervalle [a,b], l’intégrale sur cet intervalle est l’aire de la partie « coincée » entre la courbe représentative de f et l’axe des abscisse, que l’on note \(\displaystyle\int_a^b f(x)\text{d}x.\)

Le principe de la variante

On subdivise l’intervalle [a;b] en n intervalles de même largeur, égale à \(\frac{b-a}{n}\). On note ces intervalles \(I_0,\ I_1,\ …,\ I_{n-1}\) et on note \(M_k(x_k;f(x_k))\) le milieu de \(I_k\) (le « point médian »). On construit alors les rectangles de bases \(I_k\) et de hauteur \(f(x_k)\).

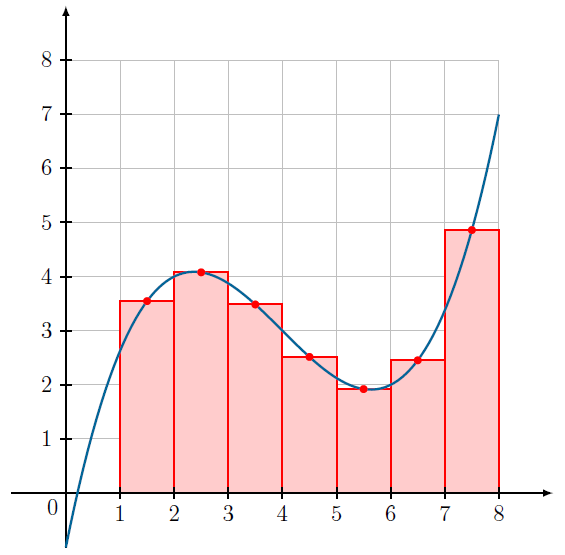
• Le premier point \(M_0\) a pour abscisse \(a + \frac{1}{2}\times\frac{b-a}{n}\), soit \(a+\frac{b-a}{2n}\), et donc pour ordonnée \(f\left(a+\frac{b-a}{2n}\right)\).
• Le deuxième point \(M_1\) a pour abscisse \(a + 3\times\frac{1}{2}\times\frac{b-a}{n}\), soit \(a+\frac{3(b-a)}{2n}\), et donc pour ordonnée \(f\left(a+\frac{3(b-a)}{2n}\right)\).
• Etc.

Plus on fait grandir n, plus les rectangles ont une base petite et plus la somme des aires des rectangles se rapproche de l’intégrale cherchée.

Implémentation en Python de la variante de la méthode des rectangles

La fonction que j’ai prise en exemple a pour expression:$$f(x)=\frac{1}{8}x^3-\frac{3}{2}x^2+5x-1.$$Je vais donc d’abord définir cette fonction:

def f(x):
    return x**3/8 - 3*x**2/2 + 5*x - 1

Ensuite je définis une fonction area(a,b,n) qui devra retourner la valeur approchée de l’intégrale cherchée sur l’intervalle [a;b] avec notre méthode, en prenant un n « assez grand ».

def area(a,b,n):
    s = 0 # somme des aires initialement nulle
    largeur = (b - a) / n
    for k in range(n):
        xk = a + (k + 0.5) * largeur # abscisse des "points médians"
        s = s + largeur * f(xk)
        
    return s

Afin de voir les différents résultats pour différentes valeurs de n, on créée une boucle sur n:

for n in range(100,2100,100):
    print("Avec n = {}, on obtient une aire de : {}.".format(n , area(1,8,n)))

Avec n = 100, on obtient une aire de : 22.968214062500007.
Avec n = 200, on obtient une aire de : 22.968616015625.
Avec n = 300, on obtient une aire de : 22.968690451388888.
Avec n = 400, on obtient une aire de : 22.968716503906258.
Avec n = 500, on obtient une aire de : 22.968728562499976.
Avec n = 600, on obtient une aire de : 22.968735112847224.
Avec n = 700, on obtient une aire de : 22.968739062499978.
Avec n = 800, on obtient une aire de : 22.96874162597657.
Avec n = 900, on obtient une aire de : 22.968743383487663.
Avec n = 1000, on obtient une aire de : 22.96874464062501.
Avec n = 1100, on obtient une aire de : 22.96874557076446.
Avec n = 1200, on obtient une aire de : 22.968746278211807.
Avec n = 1300, on obtient une aire de : 22.968746828772172.
Avec n = 1400, on obtient une aire de : 22.968747265624987.
Avec n = 1500, on obtient une aire de : 22.968747618055556.
Avec n = 1600, on obtient une aire de : 22.968747906494144.
Avec n = 1700, on obtient une aire de : 22.96874814554499.
Avec n = 1800, on obtient une aire de : 22.968748345871923.
Avec n = 1900, on obtient une aire de : 22.96874851540862.
Avec n = 2000, on obtient une aire de : 22.968748660156262.

Pour n = 100, on obtient une valeur approchée de l’intégrale au millième, mais si l’on souhaite une meilleur approximation, il faut aller jusqu’à n=2000 pour une valeur approchée au moins à \(10^{6}\) près.

Cette variante est appelée méthode du point médian.

Il existe d’autres méthodes, dont la méthode des trapèzes, dont je parle dans le livre d’exercices corrigés disponible sur ce site.